Question

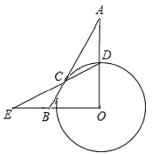
【题目】在△ABC中，∠ABC＝2∠ACB，BD平分∠ABC交AC于点D．

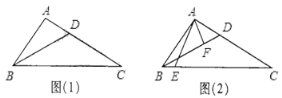
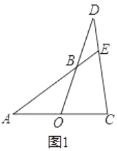
（1）如图（1），若AB＝3，AC＝5，求AD的长；

（2）如图（2），过点A分别作AC，BD的垂线，分别交BC，BD于点E，F．

①求证：∠ABC＝∠EAF；

②求的值．

Answer 1

【答案】（1）AD＝；（2）①见解析；②．

【解析】

（1）根据∠ABC＝2∠ACB，BD平分∠ABC，易得△ABD∽△ACB，利用相似三角形对应边成比例即可求解.

（2）①根据AE⊥AC，AF⊥BD，∠ABF＝∠C，易得△ABF∽△ECA，即可证得；②取CE的中点M，连接AM，在Rt△ACE中，AM＝CE，∠AME＝2∠C，由已知条件易得.

（1）∵∠ABC＝2∠ACB，BD平分∠ABC

∴∠ABD＝∠ACB.

又∠A＝∠A，

∴△ABD∽△ACB，

∴，即

∴AD＝

（2）①证明：∵AE⊥AC，AF⊥BD，

∴∠AFB＝∠EAC＝90°.

又∵∠ABF＝∠C，

∴△ABF∽△ECA，

∴∠BAF＝∠CEA.

∵∠BAF＝∠BAE＋∠EAF，∠AEC＝∠ABC＋∠BAE，

∴∠ABC＝∠EAP.

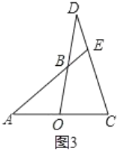
②如图，取CE的中点M，连接AM.

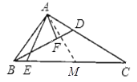
在Rt△ACE中，AM＝CE，∠AME＝2∠C.

∵∠ABC＝2∠C，

∴∠ABC＝∠AME，

∴AM＝AB，

∴．