题目内容
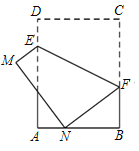
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
【答案】5或![]() .
.
【解析】
分AN=![]() AB=2与AN=
AB=2与AN=![]() AB=4两种情况讨论,设CF=NF=x,在Rt△NBF中利用勾股定理,可分别求出x的值,即CF的长度.
AB=4两种情况讨论,设CF=NF=x,在Rt△NBF中利用勾股定理,可分别求出x的值,即CF的长度.
解:由翻折知,CF=NF,
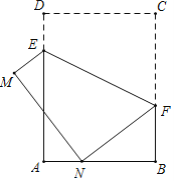
设CF=NF=x,
∵四边形ABCD为矩形,
∴∠B=90°,
当AN=![]() AB=2时,
AB=2时,
在Rt△NBF中,NF=x,BF=BC-CF=8-x,BN=AB-AN=4,
∵NF2=NB2+BF2,
∴x2=42+(8-x)2,
解得,x=5,
∴CF=5;
当AN=![]() AB=4时,
AB=4时,
在Rt△NBF中,NF=x,BF=BC-CF=8-x,BN=AB-AN=2,
∵NF2=NB2+BF2,
∴x2=22+(8-x)2,
解得,x=![]() ,
,
∴CF=![]() .
.
故答案为:5或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目