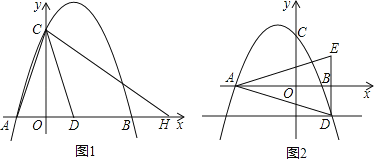题目内容
【题目】如图1,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴于点C.将直线AC以点A为旋转中心,顺时针旋转90°,交y轴于点D,交拋物线于另一点E.
与x轴交于A、B两点(点A在点B的左侧),交y轴于点C.将直线AC以点A为旋转中心,顺时针旋转90°,交y轴于点D,交拋物线于另一点E.
(1)求直线AE的解析式;
(2)点F是第一象限内抛物线上一点,当△FAD的面积最大时,求出此时点F的坐标;
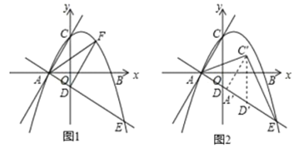
(3)如图2,将△ACD沿射线AE方向以每秒![]() 个单位的速度平移,记平移后的△ACD为△A′C′D′,平移时间为t秒,当△AC′E为等腰三角形时,求t的值.
个单位的速度平移,记平移后的△ACD为△A′C′D′,平移时间为t秒,当△AC′E为等腰三角形时,求t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由抛物线解析式,分别求出A、B、C三点坐标,由△AOC∽△DOA得![]() ,从而求出DO,进而可知直线AE的解析式;
,从而求出DO,进而可知直线AE的解析式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,分别根据抛物线和直线AE的解析式,设出点F和点K的坐标,由S△FAD=S△FAK-S△FDK,用x表示△FAD的面积,根据二次函数的性质即可求解;
,分别根据抛物线和直线AE的解析式,设出点F和点K的坐标,由S△FAD=S△FAK-S△FDK,用x表示△FAD的面积,根据二次函数的性质即可求解;
(3)连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,分三种情况讨论当△AC′E为等腰三角形时,t的值:①
,分三种情况讨论当△AC′E为等腰三角形时,t的值:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)由题意知,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,
与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,
令![]() =0,得
=0,得![]() ,所以C(0,
,所以C(0,![]() ),
),
令![]() =0,得
=0,得![]() ,所以A(-1,0),B(3,0),
,所以A(-1,0),B(3,0),
根据题意,AE⊥AC
∴∠CAD=∠CAO+∠OAD=90°,
又∵∠AOC=∠DOA=90°
∴∠OAD+∠ADO=90°
∴∠ADO=∠CAO
∴△AOC∽△DOA
∴![]()
∴![]()
∴点D的坐标为:![]()
∴直线AE的解析式为:![]() ;
;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
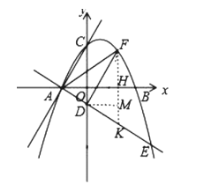
设点![]() 坐标为
坐标为![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 有最大值,
有最大值,
此时点![]() ;
;
(3)连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
则![]()
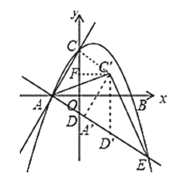
![]() 点
点![]() ,易求
,易求![]()
![]()
①当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
②当![]() 时,同理可得:
时,同理可得:![]() (舍去负值);
(舍去负值);
③当![]() 时,同理可得:
时,同理可得:![]() ;
;
故:![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】为加强公民节电意识,某县将居民用电量分为两个阶梯,月用电量不超过![]() 度时按第一个阶梯费用收费,超过
度时按第一个阶梯费用收费,超过![]() 度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 3月 |
用电量 |
|
金额 |
|
2019年3月收费员林云
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 4月 |
用电量 |
|
金额 |
|
2019年4月收费员林云