题目内容
【题目】如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
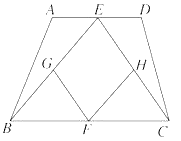
(1)证明四边形EGFH是平行四边形;(2)若EF⊥BC,且EF=![]() BC,证明平行四边形EGFH是正方形
BC,证明平行四边形EGFH是正方形
【答案】(1)平行四边形
(2)见解析
【解析】
(1)通过中位线定理得出GF∥EH且GF=EH,所以四边形EGFH是平行四边形;
(2)当添加了条件EF⊥BC,且EF=![]() BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.
证明:(1)∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=![]() EC.
EC.
又∵H是EC的中点,EH=![]() EC,
EC,
∴GF∥EH且GF=EH.
∴四边形EGFH是平行四边形.
(2)连接GH,EF.
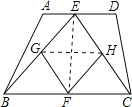
∵G,H分别是BE,EC的中点,
∴GH∥BC且GH=![]() BC.
BC.
又∵EF⊥BC且EF=![]() BC,
BC,
又∵EF⊥BC,GH是三角形EBC的中位线,
∴GH∥BC,
∴EF⊥GH,
又∵EF=GH.
∴平行四边形EGFH是正方形.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目