题目内容
证明:直角三角形斜边的中线等于斜边的一半。
证明见解析.
试题分析:作出图形,然后写出已知,求证,延长CD到E,使DE=CD,连接AE、BE,根据对角线互相平分的四边形是平行四边形判断出四边形AEBC是平行四边形,再根据有一个角是直角的平行四边形是矩形可得四边形AEBC是矩形,然后根据矩形的对角线互相平分且相等可得CD=
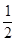 AB.
AB.试题解析:已知:如图,在△ABC中,∠ACB=90°,CD是斜边AB上的中线,

求证:CD=
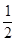 AB;
AB;证明:如图,延长CD到E,使DE=CD,连接AE、BE,
∵CD是斜边AB上的中线
∴AD=BD,
∴四边形AEBC是平行四边形,
∵∠ACB=90°,
∴四边形AEBC是矩形,
∴AD=BD=CD=DE,
∴CD=
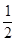 AB.
AB.考点: 直角三角形斜边上的中线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

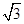
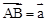 ,
,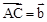 ,那么
,那么 .
.