题目内容
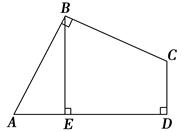
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.求证:BE=DE.

证明见解析
证明:作CF⊥BE,垂足为F,
∵BE⊥AD,
∴∠AEB=90°,
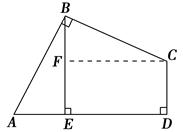
∴∠FED=∠D=∠CFE=90°,
∴四边形EFCD为矩形,
∴DE=CF,
∵∠CBE+∠ABE=90°,
∠BAE+∠ABE=90°,
∴∠BAE=∠CBF,
在△BAE和△CBF中,有∠CBE=∠BAE,∠BFC=∠BEA=90°,AB=BC,∴△BAE≌△CBF,
∴BE=CF=DE,即BE=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目