题目内容
【题目】如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m﹣7,n).
(1)求m,n的值;
(2)若点P从点C出发以每秒2个单位长度/秒的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2.是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.

【答案】(1)m=3,n=7;(2)存在,![]() <t<7
<t<7
【解析】
(1)根据点C向左平移4单位长度再向上平移7个单位长度得到对应点B,列方程组解出即可;
(2)先根据动点P、Q的速度表示出路程分别为:2t、t,再根据面积公式表示出S1和S2,代入S1<2S2列不等式求t的取值范围,并与0<t<7相结合得出t的取值.
(1)由题意得:![]()
解得:m=3,n=7,
(2)存在,如图,
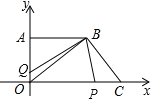
由(1)得:A(0,7),B(14,7),C(18,0),
由题意得:PC=2t,OQ=t,则OP=18-2t,
S1=![]() (AB+OP)×OA=
(AB+OP)×OA=![]() ×(14+18-2t)×7=-7t+112,
×(14+18-2t)×7=-7t+112,
S2=![]() t×14=7t,
t×14=7t,
∵要满足S1<2S2,
∴-7t+112<2×7t,
t>![]() ,
,
又∵0<t<7,
∴当![]() <t<7时,S1<2S2.
<t<7时,S1<2S2.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目