题目内容
【题目】探索规律:
观察下面由※组成的图案和算式,填空(直接写出答案):

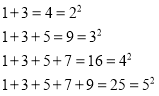
(1)请猜想1+3+5+7+9+11= ;
(2)请猜想1+3+5+7+9+……+(2n-1)= ;
(3)请用上述规律计算:41+43+45+……+97+99= .
【答案】(1)36;(2)n2;(3)2100.
【解析】
(1)根据已知得出从1开始的连续奇数之和等于数字个数的平方,进而得出答案;
(2)根据已知得出从1开始的连续奇数之和等于数字个数的平方,进而得出答案;
(3)根据题意得出原式=(1+3+5+…+97+99)-(1+3+5+…+37+39),进而求出即可.
(1)∵1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
∴1+3+5+7+9+11=62=36.
故答案为:36;
(2)1+3+5+7+9+…+(2n-1)=n2.
故答案为:n2;
(3)41+43+45+…+97+99
=(1+3+5+…+97+99)-(1+3+5+…+37+39)
=502-202
=2500-400
=2100.

【题目】学校组织八年级350名学生参加“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
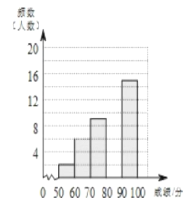
请根据所给信息,解答下列问题:
(1)求a和b的值;
(2)请补全频数分布直方图。
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.