题目内容
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
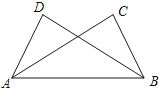
平移 |
| AA′=BB′ | |
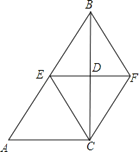
轴对称 |
| ||
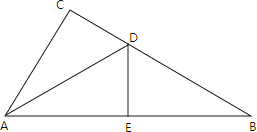
旋转 |
| AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. |
【答案】AB=A′B′,AB∥A′B′;AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.;l垂直平分AA′;OA=OA′,∠AOA′=∠BOB′.
【解析】解:①平移的性质:平移前后的对应线段相等且平行.所以与对应线段有关的结论为:AB=A′B′,AB∥A′B′;
②轴对称的性质:AA′=BB′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.
③轴对称的性质:轴对称图形对称轴是任何一对对应点所连线段的垂直平分线.所以与对应点有关的结论为:l垂直平分AA′.
④OA=OA′,∠AOA′=∠BOB′.
所以答案是:①AB=A′B′,AB∥A′B′;②AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.;③l垂直平分AA′;④OA=OA′,∠AOA′=∠BOB′.
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关,以及对平移的性质的理解,了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目