Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6．点P从点A出发，沿AC以每秒1个单位的速度向终点C运动；点Q从点C出发，沿C-B-A以每秒2个单位的速度向终点A运动．当点P停止运动时，点Q也随之停止．点P、Q同时出发，设点P的运动时间为t（秒）．

（1）求AB的长．

（2）用含t的代数式表示CP的长．

（3）设点Q到CA的距离为y，求y与t之间的函数关系式．

Answer 1

【答案】（1）10；（2）8-t； (3)y=2t(0≤t≤3)；y= (3＜t≤8)

【解析】

（1）在△ABC中，由勾股定理，求出AB的长是多少即可．

（2）首先求出AP的长度，然后用AC的长度减去AP的长度，求出CP的长度是多少即可．

（3）根据题意，分两种情况：①当0≤t≤3时；②当3＜t≤8时；求出y与t之间的函数关系式即可．

（1）如图1，

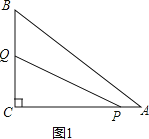
∵∠ACB=90°，AC=8，BC=6，

∴AB==10．

（2）∵点P从点A出发，沿AC以每秒1个单位的速度向终点C运动，

∴AP=t，

又∵AC=8，

∴CP=8-t．

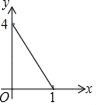
（3）①如图2，当0≤t≤3时，

，

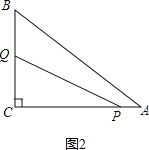∵点Q从点C出发，沿C-B-A以每秒2个单位的速度向终点A运动，

∴y=QC=2t．

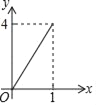
②如图3，当3＜t≤8时，如图，作QD⊥AC于点D，

，

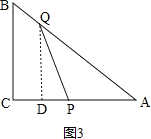∵sinA=，

∴，

∴y=-t+．