ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ½ńÄź£¬ĪŅ¹śŗ£¹Ų×ÜŹšŃĻĄ÷“ņ»÷”°Ń󥬻ų”±Ī„·ØŠŠ¶Æ£¬¼į¾ö°Ń”°Ń󥬻ų”±¾ÜÓŚ¹śĆÅÖ®ĶāČēĶ¼£¬Ä³ĢģĪŅ¹śŅ»ĖŅŗ£¼ą“¬Ń²ŗ½µ½![]() øŪæŚÕżĪ÷·½µÄ
øŪæŚÕżĪ÷·½µÄ![]() “¦Ź±£¬·¢ĻÖŌŚ
“¦Ź±£¬·¢ĻÖŌŚ![]() µÄ±±Ę«¶«
µÄ±±Ę«¶«![]() ·½Ļņ£¬Ļą¾ą
·½Ļņ£¬Ļą¾ą![]() ŗ£Ąļ“¦µÄ
ŗ£Ąļ“¦µÄ![]() µćÓŠŅ»æÉŅÉ“¬Ö»ÕżŃŲ
µćÓŠŅ»æÉŅÉ“¬Ö»ÕżŃŲ![]() ·½ĻņŠŠŹ»£¬
·½ĻņŠŠŹ»£¬![]() µćŌŚ
µćŌŚ![]() øŪæŚµÄ±±Ę«¶«
øŪæŚµÄ±±Ę«¶«![]() ·½ĻņÉĻ£¬ŗ£¼ą“¬Ļņ
·½ĻņÉĻ£¬ŗ£¼ą“¬Ļņ![]() øŪæŚ·¢³öÖøĮī£¬Ö“·Ø“¬Į¢¼““Ó
øŪæŚ·¢³öÖøĮī£¬Ö“·Ø“¬Į¢¼““Ó![]() øŪæŚŃŲ
øŪæŚŃŲ![]() ·½ĻņŹ»³ö£¬ŌŚ
·½ĻņŹ»³ö£¬ŌŚ![]() “¦³É¹¦Ą¹½ŲæÉŅÉ“¬Ö»£¬“ĖŹ±
“¦³É¹¦Ą¹½ŲæÉŅÉ“¬Ö»£¬“ĖŹ±![]() µćÓė
µćÓė![]() µćµÄ¾ąĄėĪŖ
µćµÄ¾ąĄėĪŖ![]() ŗ£Ąļ£®
ŗ£Ąļ£®
£Ø1£©Ēó![]() µÄ¶ČŹżÓė
µÄ¶ČŹżÓė![]() µćµ½Ö±Ļß
µćµ½Ö±Ļß![]() µÄ¾ąĄė£»
µÄ¾ąĄė£»
£Ø2£©Ö“·Ø“¬“Ó![]() µ½
µ½![]() ŗ½ŠŠĮĖ¶ąÉŁŗ£Ąļ£æ(½į¹ū±£ĮōøłŗÅ)
ŗ½ŠŠĮĖ¶ąÉŁŗ£Ąļ£æ(½į¹ū±£ĮōøłŗÅ)
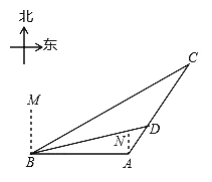
”¾“š°ø”æ£Ø1£©30”ć£¬75ŗ£Ąļ£»£Ø2£©£Ø75-25![]() £©ŗ£Ąļ£®
£©ŗ£Ąļ£®
”¾½āĪö”æ
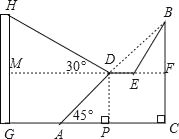
£Ø1£©øł¾ŻĢāŅāµĆ”ĻC=180”ć-30”ć-120”ć=30”ć£¬¹żµćB×÷BM”ĶCA½»CAµÄŃÓ³¤ĻßÓŚµćM£¬“Ó¶ųĒó³öBMµÄÖµ£¬¼“æɵƵ½“š°ø£»
£Ø2£©¹żµćD×÷DN”ĶBA½»BAµÄŃÓ³¤ĻßÓŚµćN£¬ÉčAD=x£¬ŌņAN=![]() x£¬DN=
x£¬DN=![]() x£¬øł¾Ż¹“¹É¶ØĄķ£¬ĮŠ³ö·½³Ģ£¬¼“æÉĒó½ā£®
x£¬øł¾Ż¹“¹É¶ØĄķ£¬ĮŠ³ö·½³Ģ£¬¼“æÉĒó½ā£®
£Ø1£©ÓÉĢāŅāµĆ£ŗ”ĻMBC=60”ć£¬”ĻABC=30”ć£¬”ĻBAC=90”ć+30”ć=120”ć£¬
”ą”ĻC=180”ć-30”ć-120”ć=30”ć£¬
¹żµćB×÷BM”ĶCA½»CAµÄŃÓ³¤ĻßÓŚµćM£¬
”ßBC=150£Øŗ£Ąļ£©£¬
”ąBM=![]() BC=
BC=![]() ”Į150=75£Øŗ£Ąļ£©£¬
”Į150=75£Øŗ£Ąļ£©£¬
¼“£ŗ![]() µćµ½Ö±Ļß
µćµ½Ö±Ļß![]() µÄ¾ąĄėĪŖ75ŗ£Ąļ£»
µÄ¾ąĄėĪŖ75ŗ£Ąļ£»
£Ø2£©¹żµćD×÷DN”ĶBA½»BAµÄŃÓ³¤ĻßÓŚµćN£¬
”ß”ĻABC=”ĻC=30”ć£¬
”ąAB=BC”Ā![]() =150”Ā
=150”Ā![]() =50
=50![]() £Øŗ£Ąļ£©£¬
£Øŗ£Ąļ£©£¬
ÉčAD=x£¬
”ß”ĻDAN=180”ć-120”ć=60”ć£¬
”ąAN=![]() x£¬DN=
x£¬DN=![]() x£¬
x£¬
”ßŌŚRtDBNÖŠ£¬![]() £¬
£¬
”ą![]() £¬½āµĆ£ŗx1=75-25
£¬½āµĆ£ŗx1=75-25![]() £¬x2=-75-25
£¬x2=-75-25![]() £ØÉįČ„£©£¬
£ØÉįČ„£©£¬
“š£ŗÖ“·Ø“¬“Ó![]() µ½
µ½![]() ŗ½ŠŠĮĖ£Ø75-25
ŗ½ŠŠĮĖ£Ø75-25![]() £©ŗ£Ąļ£®
£©ŗ£Ąļ£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø