题目内容
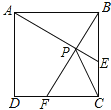
【题目】如图，在边长为2的正方形
中，动点
，
分别以相同的速度从
，
两点同时出发向和
运动(任何一个点到达停止)，在运动过程中，则线段
的最小值为________．
【答案】
【解析】
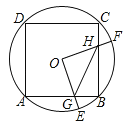
如图（见解析），先根据正方形的性质、三角形的判定定理与性质得出
，再根据正方形的性质、角的和差得出
，从而得出点P的运动轨迹，然后根据圆的性质确认CP取最小值时点P的位置，最后利用勾股定理、线段的和差求解即可．
由题意得：
由正方形的性质得：
，即
在
和
中，
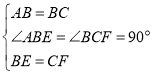
，即
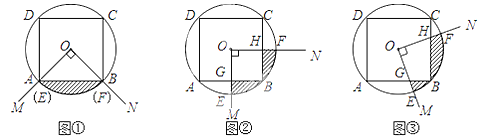
点P的运动轨迹在以AB为直径的圆弧上
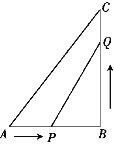
如图，设AB的中点为点O，则点P在以点O为圆心，OA为半径的圆上
连接OC，交弧AB于点Q
由圆的性质可知，当点P与点Q重合时，CP取得最小值，最小值为CQ
，即CP的最小值为
故答案为：．
练习册系列答案
相关题目
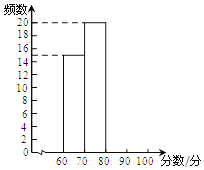
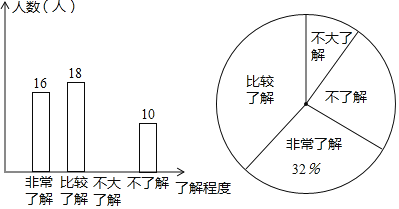
【题目】某学校组织七年级学生进行“垃圾分类”知识测试，现随机抽取部分学生的成绩进行统计，并绘制如下频数分布表以及频数分布直方图．
分数档 | 分数段/分 | 频数 | 频率 |
A | 90＜x≤100 | a | 0.12 |
B | 80＜x≤90 | b | 0.18 |
C | 70＜x≤80 | 20 | c |
D | 60＜x≤70 | 15 | d |
请根据以上信息，解答下列问题：
（1）已知A，B档的学生人数之和等于D档学生人数，求被抽取的学生人数，并把频数分布直方图补充完整．
（2）该校七年级共有200名学生参加测试，请估计七年级成绩在C档的学生人数．
（3）你能确定被抽取的这些学生的成绩的众数在哪一档吗？请说明理由．
