题目内容
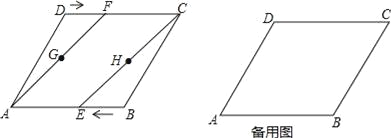
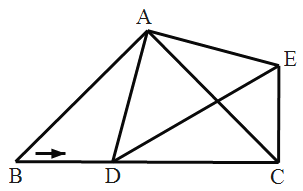
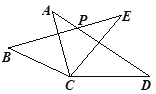
【题目】将长方形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE(如图1)；再沿过点E的直线折叠，使点D落在BE上的点D′处，折痕为EG(如图2)；再展平纸片(如图3)，则图3中∠α的大小为()
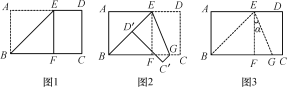
A.30°B.25.5°C.20°D.22.5°
【答案】D
【解析】
利用折叠的性质，可得∠AEB=45°，∠BEG=DEG，四边形ABFE是正方形，又由平角的定义即可求得∠DEG的度数，继而求得∠α的值．
解：根据题意得：如图③：四边形ABFE是正方形，
∴∠AEB=∠FEB=45°，
∵EG是折痕，∴∠BEG=DEG，
∵∠AEB=45°，∠AEB+∠BEG+∠DEG=180°，
∴∠DEG=67.5°，
∴∠α=90°-∠DEG=22.5°．
故选：D．
练习册系列答案
步步高达标卷系列答案
相关题目
