题目内容
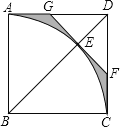
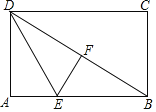
【题目】已知:如图,在矩形纸片ABCD中,![]() ,
,![]() ,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
![]() 的长为多少;
的长为多少;
![]() 求AE的长;
求AE的长;
![]() 在BE上是否存在点P,使得
在BE上是否存在点P,使得![]() 的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.
的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的长为
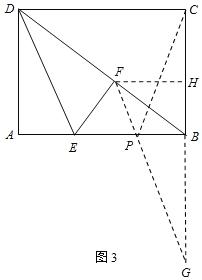
的长为![]() ;(3)存在,画出点P的位置如图3见解析,
;(3)存在,画出点P的位置如图3见解析,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)根据勾股定理解答即可;
(2)设AE=x,根据全等三角形的性质和勾股定理解答即可;
(3)延长CB到点G,使BG=BC,连接FG,交BE于点P,连接PC,利用相似三角形的判定和性质解答即可.
(1)∵矩形ABCD,∴∠DAB=90°,AD=BC=3.在Rt△ADB中,DB![]() .
.
故答案为:5;
(2)设AE=x.
∵AB=4,∴BE=4﹣x,在矩形ABCD中,根据折叠的性质知:
Rt△FDE≌Rt△ADE,∴FE=AE=x,FD=AD=BC=3,∴BF=BD﹣FD=5﹣3=2.在Rt△BEF中,根据勾股定理,得FE2+BF2=BE2,即x2+4=(4﹣x)2,解得:x![]() ,∴AE的长为
,∴AE的长为![]() ;
;
(3)存在,如图3,延长CB到点G,使BG=BC,连接FG,交BE于点P,连接PC,则点P即为所求,此时有:PC=PG,∴PF+PC=GF.
过点F作FH⊥BC,交BC于点H,则有FH∥DC,∴△BFH∽△BDC,∴![]() ,即
,即![]() ,∴
,∴![]() ,∴GH=BG+BH
,∴GH=BG+BH![]() .在Rt△GFH中,根据勾股定理,得:GF
.在Rt△GFH中,根据勾股定理,得:GF![]() ,即PF+PC的最小值为
,即PF+PC的最小值为![]() .
.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目