题目内容
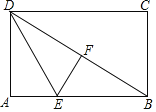
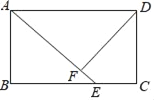
【题目】如图,已知矩形ABCD中,点E是BC边上的点,BE=2,EC=1,AE=BC,DF⊥AE,垂足为F.则下列结论:①△ADF≌△EAB;②AF=BE;③DF平分∠ADC;④sin∠CDF=![]() .其中正确的结论是_____.(把正确结论的序号都填上)
.其中正确的结论是_____.(把正确结论的序号都填上)
【答案】①②
【解析】
只要证明△EAB≌△ADF,∠CDF=∠AEB,利用勾股定理求出AB即可解决问题.
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠B=90°,
∵BE=2,EC=1,
∴AE=AD=BC=3,AB=![]() =
=![]() ,
,
∵AD∥BC,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△EAB≌△ADF,
∴AF=BE=2,DF=AB=![]() ,故①②正确,
,故①②正确,
不妨设DF平分∠ADC,则△ADF是等腰直角三角形,这个显然不可能,故③错误,
∵∠DAF+∠ADF=90°,∠CDF+∠ADF=90°,
∴∠DAF=∠CDF,
∴∠CDF=∠AEB,
∴sin∠CDF=sin∠AEB=![]() ,故④错误,
,故④错误,
故答案为①②.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目