题目内容
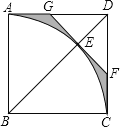
【题目】如图，在边长为2的正方形ABCD中，以B为圆心，AB为半径作扇形ABC，交对角线BD于点E，过点E作⊙B的切线分别交AD，CD于G，F两点，则图中阴影部分的面积为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由四边形ABCD是正方形，且GF是⊙B的切线可证出△DGF是等腰直角三角形，再由正方形的边长，分别知道BE的长，再求出DE的长，进一步求出DG的长．再用正方形的面积-扇形的面积-三角形的面积即可求出阴影面积．
∵四边形ABCD是正方形，
∴∠ABC=∠ADC=90°，∠GDE=∠FDE=45°，
∵GF是⊙B的切线，
∴BD⊥GF，
∴∠DEG=∠DEF=90°，
∴∠DGE=45°，∠DFE=45°，
∴DG=DF，GF=2DE，
∴DG=DF=
DE，
∵BD=AB=2，
∴DE=BD-BE=2-2，
∴DG=DF=（2-2）=4-2，
S阴影=S正方形ABCD-S扇形BAC-S△DGF
=2×2-
-
（4-2）2
=8-8-π．
故选：A．
练习册系列答案
优生乐园系列答案
相关题目
【题目】初三某班同学小戴想根据学习函数的经验，通过研究一个未学过的函数的图象，从而探究其各方面性质．
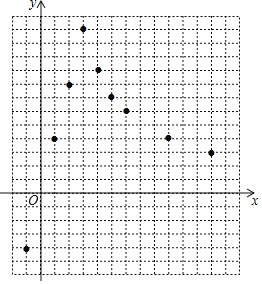
下表是函数y与自变量x的几组对应值：
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
（1）在平面直角坐标系xOy中，每个小正方形的边长为一个单位长度，描出了以上表中各对对应值为坐标的点，请根据描出的点，画出该函数的图象．
（2）请根据画出的函数图象，直接写出该函数的关系式y=______（请写出自变量的取值范围），并写出该函数的一条性质：______．
（3）当直线y=-
x+b与该函数图象有3个交点时，求b的取值范围．
