Question

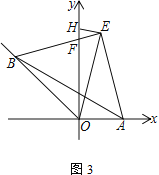
【题目】如图，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是弧AB上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，点F在线段DE上，且EF=2DF，过点C的直线CG交OA的延长线于点G，且∠CGO=∠CDE．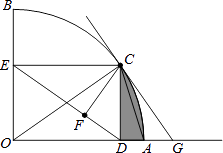
（1）求证：CG与弧AB所在圆相切．
（2）当点C在弧AB上运动时，△CFD的三条边是否存在长度不变的线段？若存在，求出该线段的长度；若不存在，说明理由．
（3）若∠CGD=60°，求图中阴影部分的面积．

Answer 1

【答案】
（1）证明：如图：

，

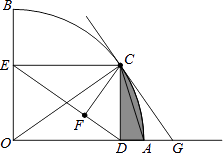∵点C作CD⊥OA于点D，作CE⊥OB于点E，

∴∠CDO=∠CEO=90°，

∵∠DOE=90°，

∴ODCE是矩形，

∴∠CDE+∠EDO=90°，∠EDO=∠COD．

∵∠CGO=∠CDE，

∴∠CGO+COD=90°，

∴∠OCG=90°，

∵CG经过半径OC的外端，

∴CG是⊙O的切线，即CG与弧AB所在圆相切

（2）解：DF不变．

在矩形ODCE中，∵DE=OC=3，EF=2DF，∴DF= DE= OC=1，

DF的长不变，DF=1

（3）解：∵∠CGD=60°，

∴∠COD=30°，

∴CD=OCsin∠COD= OC= ，OD=OCcos∠COD= OC= ，

图中阴影部分的面积 ×π×32﹣ CDOD= ﹣

【解析】（1）根据矩形的判断，可得OCDE的形状，根据矩形的性质，可得∠CDE+∠EDO=90°，∠EDO=∠COD，根据余角的性质，可得∠CGO+COD=90°，根据切线的判定，可得答案；（2）根据矩形的性质，可得CD的长，根据EF与DF的关系，可得DF的长；（3）根据锐角三角函数，可得CD、OD的长，根据根据图形割补法，可得阴影的面积．