��Ŀ����
����Ŀ�����ⴴ����ʱ���ܷ����������Ƿ�ʱ�����ƣ�ֱ�ӹ�ϵ�����˵İ�Σ��Ϊ�ռ����ȿ���֪ʶ�����ѧ���ļ�����ʶ���ֳ�����������ijУ��չ�˼���֪ʶ��У��ѵ���Ϊ�˽��ߡ����꼶ѧ��(�ߡ����꼶����600��ѧ��)����ѵЧ������У��������صļ���֪ʶ�������ִ������꼶�������ȡ20��ѧ���ļ���֪ʶ�����ɼ�(�٣�����)���з������������£�
�ռ����ݣ�
���꼶��79��85��73��80��75��76��87��70��75��94��75��78��81��72��75��80��86��59��83��77��
���꼶��92��74��87��82��72��81��94��83��77��83��80��81��71��81��72��77��82��80��70��41��
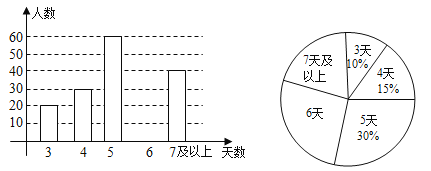
�������ݣ�
40��x��49 | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 | |
���꼶 | 0 | 1 | 0 | a | 7 | 1 |
���꼶 | 1 | 0 | 0 | 7 | b | 2 |
�������ݣ�
ƽ���� | ���� | ��λ�� | |
���꼶 | 78 | 75 | c |
���꼶 | 78 | d | 80.5 |
Ӧ�����ݣ�
��1�����ϱ���գ�a���� ����b���� ����c���� ����d���� ����
��2�����Ƹ�У�ߡ��������꼶ѧ���ڱ��ξ����гɼ���80�ּ����ϵĹ��ж����ˣ�
��3������Ϊ�ĸ��꼶��ѧ���Լ���֪ʶ���յ�����ˮƽ�Ϻã���˵�����ɣ�
���𰸡���1��11��10��78.5��81����2��600�ˣ���3�����꼶ѧ������ˮƽ�Ϻã����ɣ������꼶ƽ������ͬ�������꼶��λ��������꼶��������(��֮��������)��
��������
��1��������֪���ݼ���λ���������ĸ������ɵã�
��2������������������˼�����ɵã�
��3���𰸲�Ψһ���������ɣ�
�⣺��1��������֪a��11��b��10��
�����꼶�ɼ���������Ϊ��59��70��72��73��75��75��75��76��77��77��78��79��80��80��81��83��85��86��87��94��
�������c��![]() ��78.5��
��78.5��
���꼶�ɼ�������d��81��
�ʴ�Ϊ��11��10��78.5��81��
��2�����������ݿɵã����꼶�÷���80�ּ����ϵ�ռ![]() ��
��![]() ��
��
�����꼶�÷���80�ּ����ϵĴ�Լ600��![]() ��240�ˣ�
��240�ˣ�
���꼶�÷���80�ּ����ϵ�ռ![]() ��
��![]() ��
��
�ʰ��꼶�÷���80�ּ����ϵĴ�Լ600��![]() ��360�ˣ�
��360�ˣ�
�ʹ���600�ˣ�
��3����У���꼶ѧ���Լ���֪ʶ���յ�����ˮƽ�Ϻã�
���ɣ������꼶ƽ������ͬ�������꼶��λ��������꼶��������(��֮��������)��

����Ŀ����֪�ס������������ֱ��![]() ��
��![]() ����ͬʱ���ٳ������׳�����
����ͬʱ���ٳ������׳�����![]() �أ��ҳ�����
�أ��ҳ�����![]() �أ���ס���������
�أ���ס���������![]() �ص�·�̷ֱ�Ϊ
�ص�·�̷ֱ�Ϊ![]() ��
��![]() �����
����λ��![]() �����׳�����ʻʱ��Ϊ
�����׳�����ʻʱ��Ϊ![]() ����λ��
����λ��![]() �������׳����ٶ�Ϊ
�������׳����ٶ�Ϊ![]() ��
��![]() ��
��![]() ֮��Ķ�Ӧ��ϵ���±���
֮��Ķ�Ӧ��ϵ���±���
| 2 | 5 |
| 560 | 320 |
��1���ֱ����![]() ��
��![]() ��
��![]() ֮��ĺ�����ϵʽ������д
֮��ĺ�����ϵʽ������д![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ��ֵʱ���ס�����������������
Ϊ��ֵʱ���ס�����������������
��3������������С��![]() ʱ����
ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����Ŀ����ͼ���ڰ�![]() �У�P��ֱ��AB��һ���㣬��
�У�P��ֱ��AB��һ���㣬��![]() ������P��
������P��![]() ����
����![]() �ڵ�C��PΪ���㣬����BC������P��
�ڵ�C��PΪ���㣬����BC������P��![]() �ڵ�D��
�ڵ�D��
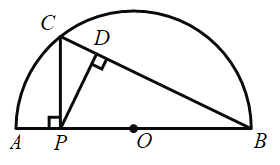
С������ѧϰ�����ľ��飬���߶�AP��CP��PD�ij���֮��Ĺ�ϵ������̽����������С����̽�����̣��벹��������
��1�����ڶ���P��AB�ϵIJ�ͬλ�ã���ͼ���������õ����߶�AP��CP��PD�ij��ȵļ���ֵ�����±���
�1 | �2 | �3 | �4 | �5 | �6 | �7 | �8 | �9 | �10 | |
| 0.37 | 0.88 | 1.59 | 2.01 | 2.44 | 3.00 | 3.58 | 4.37 | 5.03 | 5.51 |
| 1.45 | 2.12 | 2.65 | 2.83 | 2.95 | 3.00 | 2.95 | 2.67 | 2.21 | 1.65 |
| 1.40 | 1.96 | 2.27 | 2.31 | 2.27 | 2.13 | 1.87 | 1.39 | 0.89 | 0.48 |
��AP��CP��PD�ij������������У�ȷ��________�ij������Ա����� ________�ij��Ⱥ�________�ij��ȶ�������Ա����ĺ�����
��2����ͬһƽ��ֱ������ϵxOy�У�������1������ȷ���ĺ�����ͼ��
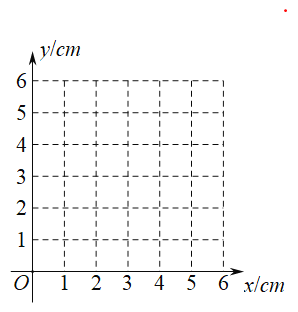
��3����Ϻ���ͼ������⣺��![]() ʱ��AP�ij���ԼΪ________��
ʱ��AP�ij���ԼΪ________��