题目内容
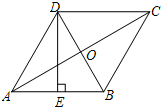
如图,在菱形ABCD中,∠BAD=72°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF=______.


连接BF,
∵四边形ABCD是菱形,
∴AD=AB,∠DAC=∠BAC=
∠BAD=
×72°=36°,
在△ADF和△ABF中,
,
∴△ADF≌△ABF(SAS),
∴∠ABF=∠ADF,
∵AB的垂直平分线交对角线AC于点F,E为垂足,
∴AF=BF,
∴∠ABF=∠BAC=36°,
∴∠ADF=36°,
∵∠ADC=180°-∠BAD=108°,
∴∠CDF=∠ADC-∠ADF=108°-36°=72°.
故答案为:72°.
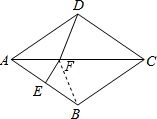
∵四边形ABCD是菱形,
∴AD=AB,∠DAC=∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
在△ADF和△ABF中,
|
∴△ADF≌△ABF(SAS),
∴∠ABF=∠ADF,
∵AB的垂直平分线交对角线AC于点F,E为垂足,
∴AF=BF,
∴∠ABF=∠BAC=36°,
∴∠ADF=36°,
∵∠ADC=180°-∠BAD=108°,
∴∠CDF=∠ADC-∠ADF=108°-36°=72°.
故答案为:72°.


练习册系列答案
相关题目