题目内容
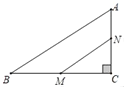
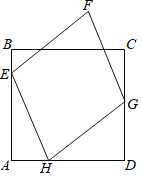
【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2.
(1)写出菱形EFGH的边长的最小值;
(2)请你探究点F到直线CD的距离为定值;
(3)连接FC,设DG=x,△FCG的面积为y;
①求y与x之间的函数关系式并求出y的取值范围;
②当x的长为何值时,点F恰好在正方形ABCD的边上.
【答案】(1)4;(2)见解析;(3)①y=6-x,6-2![]() ≤y≤6.②x=2时,点F恰好在正方形ABCD的边上.
≤y≤6.②x=2时,点F恰好在正方形ABCD的边上.
【解析】
(1)当HG⊥CD,即G与D重合时,菱形EFGH的边长最小,最小值为4.
(2)过点F作FN∥DM,根据平行公理可得FN∥AB,根据平行线的性质可以得到∠1=∠2,∠3=∠4,再根据菱形的邻角互补以及平角等于180°可以求出∠1=∠5,然后证明△AEH与△MGF全等,根据全等三角形对应边相等可得FM=AH,从而得到FM的值不会发生改变;
(3)①根据三角形的面积公式即可解决问题;
②如图连接FH、EG交于点O,作FM⊥AD于M,GN⊥AB于N,FM交GN于J,交EG于K.只要证明四边形EFGH是正方形,再证明∠EHA≌△HGD,推出DG=AH=2即可解决问题;
(1)当HG⊥CD,即G与D重合时,菱形EFGH的边长最小,
∵AD=6,AH=2,
∴DH=4,
∴菱形EFGH的边长的最小值为4.
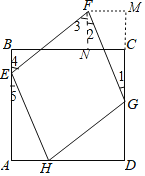
(2)作FM⊥DC交DC的延长线于M,如图,过点F作FN∥DM,
∵正方形ABCD中AB∥CD
∴FN∥AB,
∴∠1=∠2,∠3=∠4,
∵四边形EFGH是菱形,
∴∠HEF+∠GFE=180°,
即∠2+∠3+∠HEF=180°,
又∠4+∠5+∠HEF=180°,
∴∠1=∠5,
在△AEH与△MGF中,
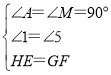 ,
,
∴△AEH≌△MGF(AAS),
∴FM=AH,
∵AH=2,
∴FM=2,是常数不变;
(3)①结合图形可得,y=![]() CGFM=
CGFM=![]() ×(6-x)×2=6-x,
×(6-x)×2=6-x,
当点G与D重合时,x=0,y=6,可得y的最大值为6
当点E与B重合时,EH=GH=![]() ,
,
在Rt△DHG中,DG=![]() ,
,
此时x=2![]() ,y=6-2
,y=6-2![]() ,可得y的最小值为6-2
,可得y的最小值为6-2![]() ,
,
∴6-2![]() ≤y≤6.
≤y≤6.
②如图连接FH、EG交于点O,作FM⊥AD于M,GN⊥AB于N,FM交GN于J,交EG于K.

∵四边形EFGH是菱形,
∴FH⊥EG,易知GN⊥FM,
∴∠FOK=∠GJK=90°,
∵∠FKO=∠GKJ,
∴∠OFK=∠JGK,
∵FM=NG,∠FMH=∠GNE=90°,
∴△FMH≌△GNE,
∴EG=FH,
∴四边形EFGH是正方形,
∴∠EHG=90°,
∵∠EHA+∠GHD=90°,∠GHD+∠HGD=90°,
∴∠EHA≌△HGD,
∴DG=AH=2.
∴x=2时,点F恰好在正方形ABCD的边上.

【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.