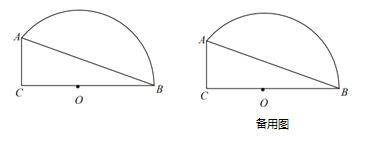��Ŀ����
����Ŀ��Ϊ�˰�ȫ����ͨ����һ������˾���������٣�ͬʱ����һ�����Ƹ�����ϵͳ����ͼ������ͭ��·ijֱ��·��MN������60ǧ��/Сʱ��Ϊ�˼����Ƿ��٣��ڹ�·MN�������˲��ٵ�C���Ӳ��ٵ�C���һС���ӵ�A�����B��ʻ��3���ӣ���֪��CAN��45������CBN��60����BC��120�ף�
��1������ٵ�C���öι�·�ľ��룻
��2������ͨ�������жϴ˳��Ƿ��٣��������ȷ��0.1m/s�����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��

���𰸡���1��60![]() ���ף�����2���˳�û�г��٣�
���ף�����2���˳�û�г��٣�
��������
��1����CH��MN����Rt��BCH�У����CH�ij������ɵò��ٵ�C���öι�·�ľ��룻��2������������Ǻ����ֱ����BH��AH�ij����������AB�ij����������ٶ�=·�̡�ʱ����øó����ٶȣ��Ƚϼ��ɽ��
��1����C��CH��MN������ΪH��
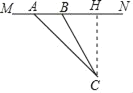
�ߡ�CBN��60����BC��120�ף�
��CH��BCsin60����120��![]() ��60
��60![]() ���ף���
���ף���
��2��BH��BCcos60����60���ף���
�ߡ�CAN��45����
��AH��CH��60![]() �ף�
�ף�
��AB��60![]() ��60��43.8��m����
��60��43.8��m����
���Ϊ43.8��3��14.6m/s��
��60ǧ��/Сʱ��16.7m/s��
�֡�14.6 m/s��16.7 m/s��
��˳�û�г��٣�

 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�����Ŀ��ij�ȼٴ�ӵ�пͷ�40�䣬�öȼٴ��ھ�Ӫ�з���ÿ��ͷ������x(Ԫ)��ÿ������Ŀͷ���(y)�����¹�ϵ��
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)�۲��������ѧ����һ�κ�������������������κ������й�֪ʶ���ÿ������Ŀͷ���y(��)��ÿ��ͷ��������x(Ԫ)֮��Ĺ�ϵʽ��
(2)��֪�����ÿ��ͷ�ÿ����Ҫ����80Ԫ��δ�����ÿ��ͷ�ÿ����Ҫ����40Ԫ����x(x��200)�Ĵ���ʽ�����
����Ŀͷ��� | ______ | δ����Ŀͷ��� | ______ |
�����ÿ��ͷ��������� | ______ | ����δ����Ŀͷ�ÿ�յ����� | ______ |
(3)�����Ǹöȼٴ���ϰ壬��Ὣÿ��ͷ��������Ϊ����Ԫ������ʹ�ȼٴ�����������棿����������Ƕ���Ԫ��