题目内容
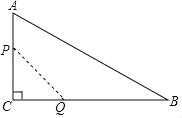
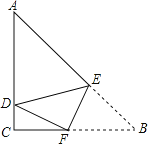
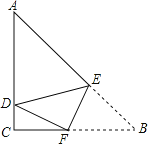
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=4,E、F分别为AB、BC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为_____.
【答案】![]() 或
或![]()
【解析】
根据题意分情况讨论,当∠ADE=90°时或当∠AED=90°时,利用相似三角形的判定和性质列比例式,从而求解.
解:在Rt△ABC中,∵∠C=90°,AB=5,AC=4,
∴BC=3.
直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,
根据折叠的性质:BE=DE
设BE=x,则DE=x,AE=10﹣x
①当∠ADE=90°时,则DE∥BC,
则△AED∽△ABC
∴![]()
∴![]()
解得:![]() ;
;
②当∠AED=90°时,∠A=∠A
则△AED∽△ACB
∴![]()
∴![]() 解得:x=
解得:x=![]()
故所求BE的长度为:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目