题目内容
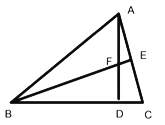
【题目】△ABC中，AB＝6，AC＝8，BC＝10，P为BC边上一动点，过线段AP上的点M作DE⊥AP，交边AB于点D，交边AC于点E，点N为DE中点，若四边形ADPE的面积为18，则AN的最大值=______．
【答案】
【解析】分析：先求APDE=36，再根据直线外一点到直线上任一点的距离，垂线段最短，利用三角形面积公式即可求得AP最短时的长，然后即可求出AN最长时的长.
详解：∵四边形ADPE的面积为18，DE⊥AP，∴
APDE=18,即APDE=36,
在△ABC中，AB=6，AC=8，BC=10，∴∠BAC=90°, ∵点N为DE中点, ∴AN=
DE, ∴DE最大时，AN最大，∵DE=
, ∴AP最小时，DE最大，即AP⊥BC时，AP最小, ∵AP=
,∴DE=
,∴AN=
. 故答案为： 
.
练习册系列答案
相关题目
【题目】滴滴公布了新的滴滴快车计价规则，车费由“总里程费+总时长费”两部分构成，不同时段收费标准不同，具体收费标准如下表，如果车费不足起步价，则按起步价收费.
时间段 | 里程费（元/千米） | 时长费（元/分钟） | 起步价（元） |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 0.80 | 0.80 | 14.00 |
（1）小明早上7:10乘坐滴滴快车上学，行车里程6千米，行车时间10分钟，则应付车费多少元？
（2）小云17:10放学回家，行车里程2千米，行车时间12分钟，则应付车费多少元？
（3）下晚自习后小明乘坐滴滴快车回家，20:45在学校上车，由于堵车，平均速度是
千米/小时，15分钟后走另外一条路回家，平均速度是
千米/小时，10分钟后到家，则他应付车费多少元？
