��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���֪�����ߵĶ�������Ϊ��2��0�����Ҿ����㣨4��1������ͼ��ֱ��y=![]() x�������߽���A��B���㣬ֱ��lΪy=��1��
x�������߽���A��B���㣬ֱ��lΪy=��1��
��1���������ߵĽ���ʽ��
��2����l���Ƿ����һ��P��ʹPA+PBȡ����Сֵ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3��֪F��x0��y0��Ϊƽ����һ���㣬M��m��n��Ϊ��������һ���㣬�ҵ�M��ֱ��l�ľ������M����F�ľ���������ȣ���F�����꣮

���𰸡���1�������ߵĽ���ʽΪy=![]() x2��x+1����2����P������Ϊ��
x2��x+1����2����P��������![]() ����1������3������F��������2��1����
����1������3������F��������2��1����
����������1���������ߵĶ�������Ϊ��2��0�������������ߵĽ���ʽΪy=a��x-2��2���������߹��㣨4��1�������ô���ϵ����������������ߵĽ���ʽ��
��2������ֱ��AB�������߽���ʽ�ɷ����飬ͨ���ⷽ����������A��B�����꣬����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ�����ݵ�B������ɵó���B������꣬���ݵ�A��B����������ô���ϵ���������ֱ��AB��Ľ���ʽ��������һ�κ���ͼ���ϵ�������������������P�����ꣻ
��3���ɵ�M��ֱ��l�ľ������M����F�ľ���������Ƚ�϶��κ���ͼ���ϵ���������������ɵó���1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
��1���������ߵĶ�������Ϊ��2��0����
�������ߵĽ���ʽΪy=a��x-2��2��
�߸������߾����㣨4��1����
��1=4a����ã�a=![]() ��
��
�������ߵĽ���ʽΪy=![]() ��x-2��2=
��x-2��2=![]() x2-x+1��
x2-x+1��
��2������ֱ��AB�������߽���ʽ�ɷ����飬�ã�
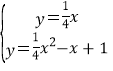 ����ã�
����ã�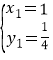 ��
��![]() ��
��
���A��������1��![]() ������B��������4��1����
������B��������4��1����
����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ����ͼ1��ʾ����
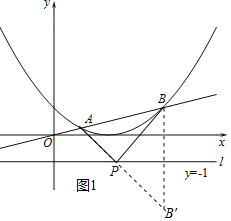
�ߵ�B��4��1����ֱ��lΪy=-1��
���B���������4��-3����
��ֱ��AB��Ľ���ʽΪy=kx+b��k��0����
��A��1��![]() ����B�䣨4��-3������y=kx+b���ã�
����B�䣨4��-3������y=kx+b���ã�
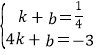 ����ã�
����ã�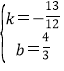 ��
��
��ֱ��AB��Ľ���ʽΪy=-![]() x+
x+![]() ��
��
��y=-1ʱ����-![]() x+
x+![]() =-1��
=-1��
��ã�x=![]() ��
��
���P��������![]() ��-1����
��-1����
��3���ߵ�M��ֱ��l�ľ������M����F�ľ���������ȣ�
�ࣨm-x0��2+��n-y0��2=��n+1��2��
��m2-2x0m+x02-2y0n+y02=2n+1��
��M��m��n��Ϊ��������һ���㣬
��n=![]() m2-m+1��
m2-m+1��
��m2-2x0m+x02-2y0��![]() m2-m+1��+y02=2��
m2-m+1��+y02=2��![]() m2-m+1��+1��
m2-m+1��+1��
�������1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
��mΪ����ֵ��
��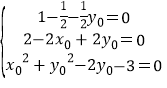 ��
��
��![]() ��
��
�ඨ��F������Ϊ��2��1����

 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�����Ŀ��ijУ����1000��ѧ����Ϊ���˽����ǵ�����������������˲���ѧ������������������������������Ƴ�ֱ��ͼ������ͼ.

��1����ι������˶�����ѧ��������ͼ�е�![]() ��
��![]() ֵ�ֱ��Ƕ��٣�
ֵ�ֱ��Ƕ��٣�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���ڹ��߽ϰ��Ļ�����ѧϰ��ѧ��ռ��Ӧ������ѧ���ı������±���
���� |
| 0.35��0.65 | 0.65��0.95 | 0.95��1.25 | 1.25��l.55 |
���� |
|
|
|
|
|
���ݵ��������Ƹ�У�ж���ѧ���ڹ��߽ϰ��Ļ�����ѧϰ��







