Question

（1）解不等式

2x-1

3

≤

5x+1

2

+1，并把它的解集在数轴上（如图1）表示出来．
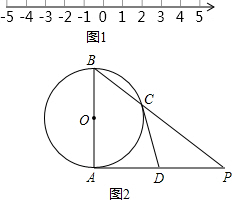
（2）如图2，已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，点D为AP的中点．直线CD是⊙O的切线吗？说明理由．

Answer 1

分析：（1）根据不等式的步骤：一、去分母（有括号的先去括号）二、移项三、合并同类项四、将未知数的系数变为1（注意不等式左边是负号时，要改变不等号的方向）
根据以上步骤解答即可．
（2）本题连接OC，证出OC⊥CD即可．首先连接AC，得出直角三角形ACP，根据直角三角形斜边上中线等于斜边一半得CD=AD，再利用等腰三角形性质可证∠OCD=∠OAD=90°，从而解决问题．

解答：解：2（2x-1）≤3（5x+1）+6，
4x-2≤15x+3+6，
-11x≤11，
x≥-1，
在数轴上表示如图所示：

（2）如图，连接OC、AC．
∵AB是⊙O的直径，
∴∠BCA=90°，又∵∠ACP=180°-∠BCA=90°．
在Rt△APC中，D为AP的中点，
∴CD=

1

2

AP=AD．
∴∠4=∠3．
又∵OC=OA，
∴∠1=∠2．
∵∠2+∠4=∠PAB=90°，
∴∠1+∠3=∠2+∠4=90°．
即OC⊥CD．
∴直线CD是⊙O的切线．

点评：（1）此题主要考查了运用解不等式的基本步骤来求解，并会在图上表示；
（2）本题综合考查了圆周角定理、切线的判定与性质．注意掌握辅助线的作法．