题目内容
(1)解方程组x-
=
-1
(2)解方程组
(3)解不等式
-
≤
-1并把解集在数轴上表示出来.
| 1-x |
| 3 |
| x+2 |
| 6 |
(2)解方程组
|
(3)解不等式
| 2x-1 |
| 4 |
| x-2 |
| 3 |
| 4x+3 |
| 6 |
分析:(1)根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解;
(2)利用加减消元法求解即可;
(3)根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.
(2)利用加减消元法求解即可;
(3)根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.
解答:解:(1)去分母得,6x-2(1-x)=x+2-6,
去括号得,6x-2+2x=x+2-6,
移项得,6x+2x-x=2-6+2,
合并同类项得,7x=-2,
系数化为1得,x=-
;
(2)
,
①×3得,6x+9y=21③,
②×2得,6x-10y=2④,
③-④得,19y=19,
解得y=1,
把y=1代入①得,2x+3=7,
解得x=2,
所以,方程组的解是
;
(3)去分母得,3(2x-1)-4(x-2)≤2(4x+3)-12,
去括号得,6x-3-4x+8≤8x+6-12,
移项得,6x-4x-8x≤6-12+3-8,
合并同类项得,-6x≤-11,
系数化为1得,x≥
,
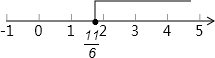
在数轴上表示如下:
去括号得,6x-2+2x=x+2-6,
移项得,6x+2x-x=2-6+2,
合并同类项得,7x=-2,
系数化为1得,x=-
| 2 |
| 7 |
(2)
|
①×3得,6x+9y=21③,
②×2得,6x-10y=2④,
③-④得,19y=19,
解得y=1,
把y=1代入①得,2x+3=7,
解得x=2,
所以,方程组的解是
|
(3)去分母得,3(2x-1)-4(x-2)≤2(4x+3)-12,
去括号得,6x-3-4x+8≤8x+6-12,
移项得,6x-4x-8x≤6-12+3-8,
合并同类项得,-6x≤-11,
系数化为1得,x≥
| 11 |
| 6 |
在数轴上表示如下:

点评:(1)主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;
(2)考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单;
(3)考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错,解不等式要依据不等式的基本性质:
①不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
②不等式的两边同时乘以或除以同一个正数不等号的方向不变;
③不等式的两边同时乘以或除以同一个负数不等号的方向改变.
(2)考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单;
(3)考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错,解不等式要依据不等式的基本性质:
①不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
②不等式的两边同时乘以或除以同一个正数不等号的方向不变;
③不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)解方程组:
(1)解方程组: