��Ŀ����
����Ŀ����δ��С�������г��Ӽҳ�����Ұ�⽼�Σ��Ӽҳ���0.5Сʱ����أ�����һ��ʱ���ԭ��ǰ���ҵأ�С�����1Сʱ20���Ӻ�����ݳ�����ͬ·��ǰ���ҵأ���ʻ10����ʱ��ǡ�þ����أ���ͼ�����Ǿ��ҵص�·��y��km����С�����ʱ��x��h���ĺ���ͼ��
��1��С���ﳵ���ٶ�Ϊ�� ��km/h��H������Ϊ�� ����
��2����С������һ��ʱ���ǰ���ҵصĹ�����y��x�ĺ�����ϵ��
��3��С���Ӽҳ�������Сʱ�������ϣ���ʱ��ҵ�·�̶�Զ��

���𰸡���1��20����![]() ��20������2��y2����20x+40����3��1.75Сʱ��25km��
��20������2��y2����20x+40����3��1.75Сʱ��25km��
��������
��1�����ݺ���ͼ�е����ݣ���С���Ӽҵ��ص�·�̺�ʱ��������С���ﳵ���ٶȣ���2�������ֱ��AB�Ľ���ʽ���ٸ���ֱ��AB��CD�����ֱ��CD�Ľ���ʽ��
��3�����ֱ��EF�Ľ���ʽ������ֱ��CD��ֱ��EF�Ľ���ʽ���������D�����꼴�ɣ�
�⣺��1���ɺ���ͼ���Եó���С���Ҿ���ص�·��Ϊ10km������ʱ��Ϊ0.5h��
��С���ﳵ���ٶ�Ϊ��10��0.5��20��km/h����
������ɵó�����H��������Ϊ20��������Ϊ��![]() =
=![]() ��
��
�ʵ�H������Ϊ��![]() ��20����
��20����
�ʴ�Ϊ��20����![]() ��20����
��20����
��2����ֱ��AB�Ľ���ʽΪ��y1��k1x+b1��
����A��0��30����B��0.5��20������ã�y1����20x+30��
��AB��CD��
����ֱ��CD�Ľ���ʽΪ��y2����20x+b2��
����C��1��20������ã�b2��40��
��y2����20x+40��
��3����ֱ��EF�Ľ���ʽΪ��y3��k3x+b3��
����E��![]() ��30����H (
��30����H (![]() ,20)����ã�k3����60��b3��110��
,20)����ã�k3����60��b3��110��
��y3����60x+110��
�ⷽ����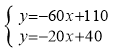 �����
�����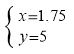 ��
��
���D������1.75��5����
30��5��25��km����
����С������1.75Сʱ�������ϣ���ʱ���25km��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�






