题目内容
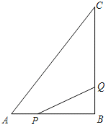
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE;
(2)由(1)知△ADE≌△FCE,得到AE=EF,AD=CF,由于AB=BC+AD,等量代换得到AB=BC+CF,即AB=BF,证得△ABE≌△FBE,即可得到结论.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
 ,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,
在△ABE与△FBE中,
 ,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AF.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目