题目内容
【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE,CN、BE交于点P. 求证:∠ANC = ∠ABE.
应用:Q是线段BC的中点,连结PQ. 若BC = 6,则PQ = ___________.

【答案】(1)证明见解析;(2)PQ=3
【解析】试题分析:根据正方形性质得出AN=AB,AC=AE,∠NAB=∠CAE=90°,求出∠NAC=∠BAE,证出△ANC≌△ABE即可.
试题解析:(1)∵四边形ANMB和ACDE是正方形,
∴AN=AB,AC=AE,∠NAB=∠CAE=90°,
∵∠NAC=∠NAB+∠BAC,∠BAE=∠BAC+∠CAE,
∴∠NAC=∠BAE,
在△ANC和△ABE中
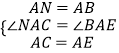
∴△ANC≌△ABE(SAS),
∴∠ANC=∠ABE.
(2)∵四边形NABM是正方形,
∴∠NAB=90°,
∴∠ANC+∠AON=90°,
∵∠BOP=∠AON,∠ANC=∠ABE,
∴∠ABP+∠BOP=90°,
∴∠BPC=∠ABP+∠BOP=90°,
∵Q为BC中点,BC=6,
∴PQ=![]() BC=3,
BC=3,
故答案为:3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目