题目内容
【题目】已知射线![]() 是
是![]() 的角平分线,
的角平分线,![]() ,点
,点![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() .
.
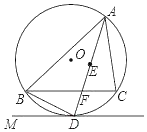
(1)如图1,当点![]() 在射线
在射线![]() 上时,连接
上时,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 的形状是_____.
的形状是_____.
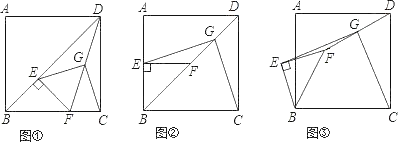
(2)如图2,当点![]() 在射线
在射线![]() 的反向延长线
的反向延长线![]() 上时,连接
上时,连接![]() ,
,![]() .若
.若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.

【答案】(1)等边三角形;(2)成立,理由见解析.
【解析】
(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CB,即可得出结论;
(2)作CE⊥AM于E,作CF⊥AN于F,根据角平分线的性质得到 CE=CF,
再根据∠ABC=∠ADC,证明△BCF≌△DCE,得到BC=CD即可证明.
(1)∵射线AC是∠MAN的角平分线,∠NAC=60°,
∴∠MAN=120°,
∵∠ABC=∠ADC=90°,
根据四边形的内角和得,∠BCD=360°(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB(角平分线的性质定理),
∴△BCD是等边三角形;
(2)成立,如图所示,作CE⊥AM于E,作CF⊥AN于F,
∵AC是∠NAM的角平分线,CE⊥AM,CF⊥AN,
∴CE=CF,
∵∠ABC=∠ADC,
∴△BCF≌△DCE,
∴BC=CD,
∵∠BCD=∠BAD=60°,
∴△BCD是等边三角形.


练习册系列答案
相关题目