题目内容
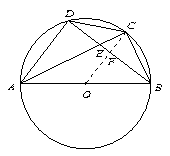
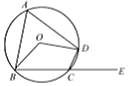
(本题满分8分)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为BD弧的中点,AC、BD交于点E.
(1)求证:△CBE∽△CAB;
(2)若S△CBE∶S△CAB=1∶4,求sin∠ABD的值.
(1)求证:△CBE∽△CAB;
(2)若S△CBE∶S△CAB=1∶4,求sin∠ABD的值.

(1)证明:∵点C为弧BD的中点,∴∠DBC=∠BAC,
在△CBE与△CAB中;
∠DBC=∠BAC,∠BCE=∠ACB,
∴△CBE∽△CAB. ……4分
(2)解:连接OC交BD于F点,则OC垂直平分BD
∵S△CBE:S△CAB=1:4,△CBE∽△CAB
∴AC:BC=BC:EC=2:1,∴AC=4EC
∴AE:EC=3:1
∵AB为⊙O的直径,∴∠ADB=90°
∴AD∥OC,则AD:FC=AE:EC=3:1
设FC=a,则AD=3a,
∵F为BD的中点,O为AB的中点,
∴OF是△ABD的中位线,则OF=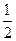 AD=1.5a,
AD=1.5a,
∴OC=OF+FC=1.5a+a=2.5a,则AB=2OC=5a,
在Rt△ABD中,sin∠ABD= =
=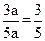 …………………………8分
…………………………8分
(本题方法众多,方法不唯一,请酌情给分)

在△CBE与△CAB中;
∠DBC=∠BAC,∠BCE=∠ACB,
∴△CBE∽△CAB. ……4分
(2)解:连接OC交BD于F点,则OC垂直平分BD
∵S△CBE:S△CAB=1:4,△CBE∽△CAB
∴AC:BC=BC:EC=2:1,∴AC=4EC
∴AE:EC=3:1
∵AB为⊙O的直径,∴∠ADB=90°
∴AD∥OC,则AD:FC=AE:EC=3:1
设FC=a,则AD=3a,
∵F为BD的中点,O为AB的中点,
∴OF是△ABD的中位线,则OF=
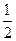 AD=1.5a,
AD=1.5a, ∴OC=OF+FC=1.5a+a=2.5a,则AB=2OC=5a,
在Rt△ABD中,sin∠ABD=
 =
=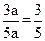 …………………………8分
…………………………8分(本题方法众多,方法不唯一,请酌情给分)
略

练习册系列答案
相关题目
 与
与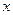 轴相切于点
轴相切于点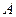 ,与
,与 轴相交于点
轴相交于点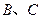 两点,连结
两点,连结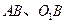 。
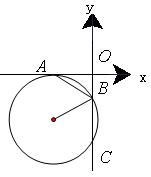
。
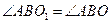 ;
;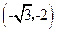 ,直接写出点
,直接写出点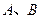 两点作⊙
两点作⊙ 与
与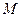 ,与
,与 的延长线交于点
的延长线交于点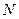 ,当⊙
,当⊙
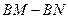 的值不变;②
的值不变;②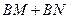 的值不变;
的值不变;
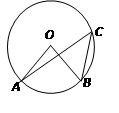
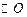 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和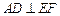 ,垂足为D.
,垂足为D.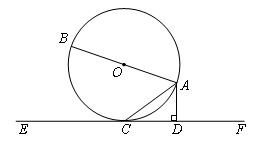
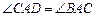 ;
;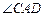 相等的角?若存在,找出一个这样
相等的角?若存在,找出一个这样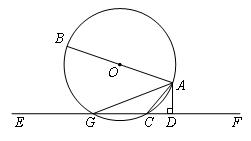
 O′交
O′交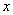 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F. 腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.