题目内容
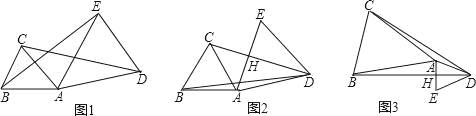
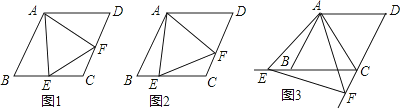
【题目】如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.

【答案】图中阴影部分的面积为![]() .
.
【解析】试题分析:
如图,设点C在BD上的对应点为点F,连接EF,则易得EF⊥BD于点F,BF=BC=12,由已知易得BD=13,由此可得DF=1,设CE=x,则EF=x,DE=5-x,在Rt△DEF中由勾股定理建立方程即可求得x的值,从而可得到EF的长,结合BD的长即可求出△BDE的面积了.
试题解析:
设折叠后点C在BD上的对应点为点F,连接EF,
∴EF⊥BD,BF=BC=12,
∴∠DFE=90°,
∵AB=5,AD=BC=12,∠A=90°,
∴BD=![]() ,
,
∴DF=13-12=1,
设CE=x,则EF=CE=x,DE=5-x,
在△DEF中,x2+12=(5-x)2,
解得x=![]() ,
,
∴图中阴影部分的面积S△BDE=![]() ×13×
×13×![]() =
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
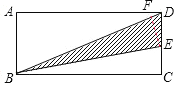
【题目】为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
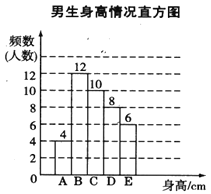
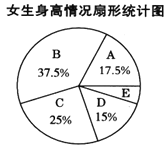
根据图表提供的信息,回答下列问题:
(1)样本中,男生身高的众数在___________组,中位数在___________组;
(2)样本中,女生身高在E组的有___________人;
(3)已知该校共有男生400人、女生380人,请估计身高在160≤x<170范围内的学生约有多少人.