Question

【题目】如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边正方形EFGH的周长为（ ）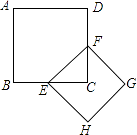

A.
B.2
C.
+1
D.2 +1

Answer 1

【答案】B
【解析】解：∵正方形ABCD的面积为1，
∴BC=CD= =1，∠BCD=90°，
∵E、F分别是BC、CD的中点，
∴CE= BC= ，CF= CD= ，
∴CE=CF，
∴△CEF是等腰直角三角形，
∴EF= CE= ，
∴正方形EFGH的周长=4EF=4× =2 ；
故选：B．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．