Question

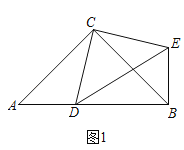
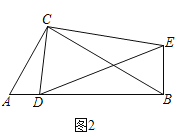
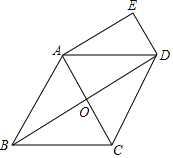
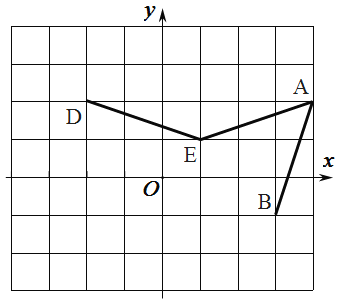
【题目】如图，在边长为1的正方形网格中，，，，，绕点顺时针旋转得（点与点对应）.

（1）直接写出的值： ；

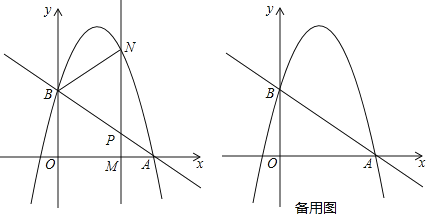
（2）用无刻度直尺作出点并直接写出的坐标（保留作图痕迹，不写作法）；

（3）若格点在的角平分线上，这样的格点（不包括点有） 个（直接写出答案）

Answer 1

【答案】（1）90；（2）见解析（3）5

【解析】

（1）找出旋转中心C后，利用勾股定理可证明旋转角∠AOE是90°

（2）根据旋转的性质,对应点到旋转中心的距离相等,可知,只要连接两组对应点,作出对应点所连线段的两条垂直平分线,其交点即为旋转中心；

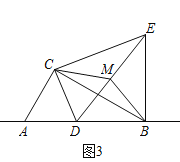
（3）取M(-1，-1)可证 故∠EAM=∠BAM故AM是的角平分线上，数出在格子点上的格点（不包括点）的个数即可.

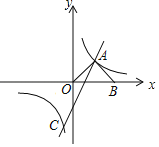
解：（1）由题意，作出旋转中心C（2，3），

∵

又∵

∴

∴∠AOE=90°

∴；

故答案为:90°

（2）如图：

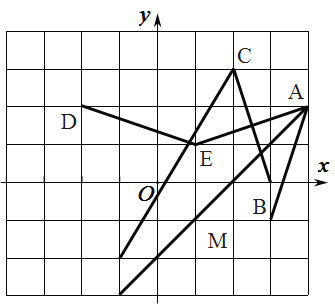
(3)∵A(4,2) ，,M(-1，-1)

∴EM=BM=2，AE=AB=

∵AM=AM

∴

∴∠EAM=∠BAM

∴AM是的角平分线上

由图可知AM在格子点上的格点（不包括点）有5个