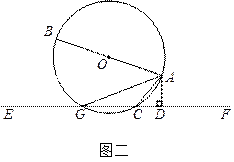题目内容
如图,直线 与
与 轴、
轴、 轴分别相交于
轴分别相交于 两点,圆心
两点,圆心 的坐标为
的坐标为 ,圆
,圆 与
与 轴相切于点
轴相切于点 .若将圆
.若将圆 沿
沿 轴向左移动,当圆
轴向左移动,当圆 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点 的个数是( )
的个数是( )

 与
与 轴、
轴、 轴分别相交于
轴分别相交于 两点,圆心
两点,圆心 的坐标为
的坐标为 ,圆
,圆 与
与 轴相切于点
轴相切于点 .若将圆
.若将圆 沿
沿 轴向左移动,当圆
轴向左移动,当圆 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点 的个数是( )
的个数是( )
| A.2 | B.3 | C.4 | D.5 |
B
因为是动点,所以从特殊位置(相切)入手分析,分右相切和左相切两种情况,然后求解.
解:若圆和直线相切,则圆心到直线的距离应等于圆的半径1,
据直线的解析式求得A(-3,0),B(0,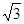 ),
),
则tan∠BAO=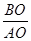 =
= ,
,
所以∠BAO=30°,
所以当相切时,AP=2,
点P可能在点A的左侧或右侧.所以要相交,应介于这两种情况之间,即需要移动的距离>4-2=2,而<3+2=5,此时横坐标为整数的点P有(-2,0)(-3,0)(-4,0)三个.
故答案为3.
注意:本题正确答案为3,有许多学生把直线与圆相切的点也看成交点,得到答案是5;也有的学生只考虑⊙P在线段OA之间运动,得到答案为2.
解:若圆和直线相切,则圆心到直线的距离应等于圆的半径1,
据直线的解析式求得A(-3,0),B(0,
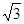 ),
),则tan∠BAO=
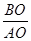 =
= ,
,所以∠BAO=30°,
所以当相切时,AP=2,
点P可能在点A的左侧或右侧.所以要相交,应介于这两种情况之间,即需要移动的距离>4-2=2,而<3+2=5,此时横坐标为整数的点P有(-2,0)(-3,0)(-4,0)三个.
故答案为3.
注意:本题正确答案为3,有许多学生把直线与圆相切的点也看成交点,得到答案是5;也有的学生只考虑⊙P在线段OA之间运动,得到答案为2.

练习册系列答案
相关题目



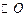 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和 ,垂足为D.
,垂足为D.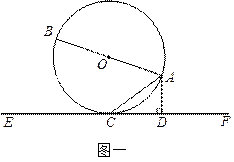
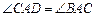 ;
;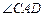 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.