题目内容
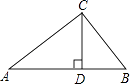
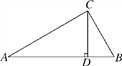
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的面积记作S2 , 照此规律作下去,则S1= , S2017= . 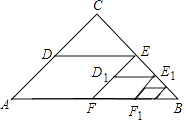
【答案】1;![]()
【解析】解:∵∠C=90°,AC=BC=2,
∴△ABC的面积为: ![]() ×2×2=2,
×2×2=2,
∵点E为BC边中点,ED∥AB,
∴△CDE∽△CAB,
∴ ![]() =
= ![]() ,
,
∴S△CDE= ![]() ,
,
∵EF∥AC,点E为BC边中点,
∴S△BEF= ![]() ,
,
∴S1=1,
同理,S2= ![]() ,S3=
,S3= ![]() ,
,
以此类推,S2017= ![]() .
.
所以答案是:1; ![]() .
.
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目