题目内容
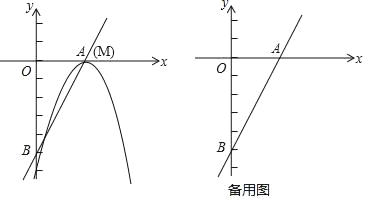
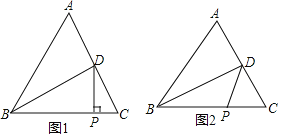
【题目】如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
(1)线段AC的长=________;
(2)当△PCF与△EDF相似时,求t的值.

【答案】6
【解析】试题分析:(1)作EH⊥AC于H,如图,易得四边形CDEH为矩形,从而得到CH=DE=2,EH=CD=3,然后利用勾股定理计算出![]() 即可得到
即可得到![]() 的长;
的长;
(2)![]() 则
则![]() 由于
由于![]() 根据两组对应边的比相等且夹角对应相等的两个三角形相似可分类讨论:若当
根据两组对应边的比相等且夹角对应相等的两个三角形相似可分类讨论:若当![]() 时,△CFP∽△DFE,
时,△CFP∽△DFE, ![]() 时,△CFP∽△DEF,然后分别利用相似比得到关于
时,△CFP∽△DEF,然后分别利用相似比得到关于![]() 的方程,再解方程求出
的方程,再解方程求出![]() 即可.
即可.
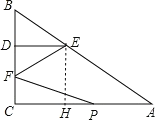
试题解析:(1)作EH⊥AC于H,如图,
![]()
∴四边形CDEH为矩形,
∴CH=DE=2,EH=CD=3,
在![]() 中,
中, ![]()
∴AC=CH+AH=2+4=6;
(2)CF=t,PA=2t,则DF=3t,CP=62t,0<t<3,
∵∠C=∠FDE,
∴当![]() 时,△CFP∽△DFE,即
时,△CFP∽△DFE,即![]() 整理得
整理得![]() 解得
解得 ![]() (舍去),
(舍去),
∴当![]() 时,△CFP∽△DEF,即
时,△CFP∽△DEF,即![]() 整理得
整理得![]() (舍去).
(舍去).
综上所述,t的值为![]()

 阅读快车系列答案
阅读快车系列答案【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.