题目内容
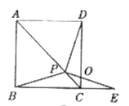
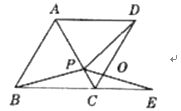
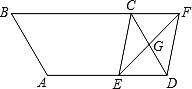
【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为![]()
(1)求证:无论![]() 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;
(2)①当![]() s时,CE⊥AD;
s时,CE⊥AD;
②当![]() 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.
【答案】(1)见解析;(2)①3.5;②2.
【解析】
(1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可;
(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,即可得出答案;
②求出△CDE是等边三角形,推出CE=DE,即可得出答案.
(1)四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
又∠CGF=∠EGD.
G是CD的中点,
CG=DG,
在△FCG和△EDG中,
∵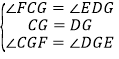 ,
,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)①当t=3.5s时,CE⊥AD,
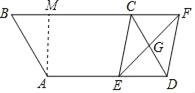
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
∵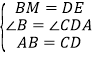 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
即CE⊥AD,
故答案为:3.5;
②当t=2s时,平行四边形CEDF的两条邻边相等,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
即平行四边形CEDF的两条邻边相等,
故答案为:2.

【题目】空气质量指数是国际上普遍采用的定量评价空气质量好坏的重要指标,空气质量指数不超过50则空气质量评估为优.下表记录了我市11月某一周7天的空气质量指数变化情况.规定:空气质量指数50记为零,空气质量指数超过50记为正,空气质量指数低于50记为负.
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
+18 | ﹣4 | ﹣1 | ﹣18 | ﹣10 | +28 | +29 |
解答以下问题:
(1)根据表格可知,星期四空气质量指数为 ,星期六比星期二空气质量指数高 ;
(2)求这一周7天的平均空气质量指数.