题目内容
【题目】如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 . 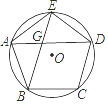
【答案】![]() ﹣1
﹣1
【解析】解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,
∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴AE2=EGEB,
∴22=x(x+2),
解得x=﹣1+ ![]() 或﹣1﹣
或﹣1﹣ ![]() ,
,
∴EG= ![]() ﹣1,
﹣1,
故答案为 ![]() ﹣1.
﹣1.
根据已知先证明AB=BG=AE=2;∠AEG=∠AEB,∠EAG=∠EBA,根据相似三角形的判定证明△AEG∽△BEA,再根据相似三角形的性质得出AE2=EGEB,建立方程求解,即可得出EG的长。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目