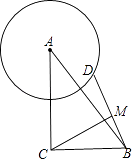题目内容
【题目】如图,在△ABC中,OA=8,OB=6,C点与A点关于直线OB对称,动点P、Q分别在线段AC、AB上(点P不与点A.C重合),满足∠BPQ=∠BAO.
(1)当OP=_______时,△APQ≌△CBP,说明理由;
(2)当△PQB为等腰三角形时,求OP的长度.

【答案】(1)2,理由见解析;(2)OP2或![]() .
.
【解析】
(1)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(2)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)当OP=2时,△APQ≌△CBP.
理由如下:
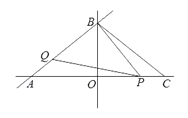
∵OA=8,OB=6,C点与A点关于直线OB对称,
∴![]() ,
,
∵OA=8,OP=2,
∴AP=BC=10
∵C点与A点关于直线OB对称,
∴∠BAO=∠BCO
∵∠BPQ=∠BAO,
∴∠BPQ=∠BCO
∵∠APB=∠APQ+∠BPQ=∠BCO+∠CBP,
∴∠APQ=∠CBP
在△APQ和△CBP中
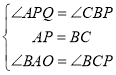 ,
,
∴△APQ≌△CBP(ASA)
(2)分为3种情况:
①当PB=PQ时,
由(1)得:△APQ≌△CBP时,PB=PQ此时OP=2;
②当BQ=BP时,
∠BPQ=∠BQP
∵∠BPQ=∠BAO,
∴∠BAO=∠BQP
根据三角形外角性质得:∠BQP>∠BAO,
∴这种情况不存在;
③当QB=QP时,
∠QBP=∠BPQ=∠BAO,
∴PB=PA,
设OP=x,则PB=PA=x+8
在Rt△OBP中,PB2=OP2+OB2,
∴(8+x)2=x2+62
解得:x![]() ;
;
∵点P在AC上,
∴点P在点O左边,
此时OP![]() ;
;
∴当△PQB为等腰三角形时,OP2或![]() ;
;

练习册系列答案
相关题目