题目内容
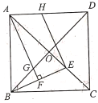
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,且AB=AE,过点A作AF⊥BE,垂足为F,交BD于点G.点H在AD上,且EH∥AF.若正方形ABCD的边长为2,下列结论:①OE=OG;②EH=BE;③AH=![]() ,其中正确的有( )
,其中正确的有( )
A. 0个B. 1个C. 2个D. 3个
【答案】D
【解析】
根据正方形的性质及全等三角形的判定与性质即可分别求证判断.
在正方形ABCD中,AO=BO,∠AOG=∠BOE,AC⊥BD
∵AF⊥BE,∴∠EAF+∠BEO=∠BEO+∠OBE=90°,
∴∠OAG=∠OBE,∴△OAG≌△OBE,故OE=OG,①正确;
∵AB=AE,∴∠ABE=∠AEB,
∵EH∥AF∴HE⊥BE,
∴∠AEF+∠AEH=∠ABE+∠CBE,∴∠AEH=∠CBE
又∵AE=AB=CB,∠HAE=∠ECB=45°,∴△AEH≌△CBE,
∴EH=BE,②正确;
∵△AEH≌△CBE,AC=![]()
∴AH=CE=AC-AE=![]() -2,③正确.
-2,③正确.
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目