题目内容
【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
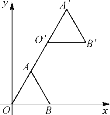
A. (4,2![]() ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2)
【答案】A
【解析】
作AM⊥x轴,根据等边三角形的性质得出OA=OB=2,∠AOB=60°,利用含30°角的直角三角形的性质求出OM=![]() OA=1,即可求出AM的长,进而可得A点坐标,即可得出直线OA的解析式,把x=3代入可得A′点的坐标,由一对对应点A与A′的移动规律即可求出点B′的坐标.
OA=1,即可求出AM的长,进而可得A点坐标,即可得出直线OA的解析式,把x=3代入可得A′点的坐标,由一对对应点A与A′的移动规律即可求出点B′的坐标.
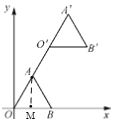
如图,作AM⊥x轴于点M,
∵等边△OAB的顶点B坐标为(2,0),
∴OA=OB=2,∠AOB=60°,
∴OM=![]() OA=1,AM=
OA=1,AM=![]() OM=
OM=![]() ,
,
∴A(1,![]() ),
),
∴直线OA的解析式为:y=![]() x,
x,
∴当x=3时,y=3![]() ,
,
∴A′(3,3![]() ),
),
∴将A点向右平移2个单位,再向上平移2![]() 个单位后得到A′点,
个单位后得到A′点,
∴将B(2,0)向右平移2个单位,再向上平移2![]() 个单位后可得到B′点,
个单位后可得到B′点,
∴点B′的坐标为(4,2![]() ),
),
故选A

【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
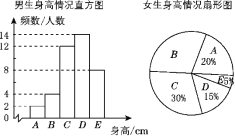
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.