题目内容
【题目】某中学要在一块三角形花圃里种植两种不同的花草,同时拟从A点修建一条小路到边BC.
(1)若要使修建小路所用的材料最少,请在下图中画出小路AD;
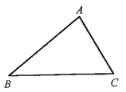
(2)若要使小路两侧种植不同花草的面积相等,请在下图中画出小路AE,其中E点满足的条件是________,并说明理由.
【答案】(1)详见解析;(2)点E为线段BC的中点,理由详见解析
【解析】
(1)根据垂线段的性质,可得答案;
(2)根据三角形中线的性质,可得答案.
(1)如图所示,过点A作AD⊥BC于点D,由“垂线段最短”可知,小路AD是所用材料最少的.
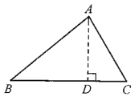
(2)点E为线段BC的中点.如图所示,找出线段BC的中点E,连接AE,AE即为所要求的小路的路径.
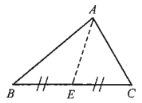
理由:∵![]() 和
和![]() 对它们的底边来说具有相同的高,同设为h.
对它们的底边来说具有相同的高,同设为h.
又∵E是BC的中点,即![]() .
.
![]() .
.
即修建小路AE可以确保两侧种植不同花草的面积相等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?