��Ŀ����
����Ŀ����ͼ��ֱ��y����![]() x+4��x�ύ�ڵ�A����y���ڵ�C����֪���κ�����ͼ����A��C�͵�B����1��0����
x+4��x�ύ�ڵ�A����y���ڵ�C����֪���κ�����ͼ����A��C�͵�B����1��0����
��1����ö��κ����Ĺ�ϵʽ��
��2����ö��κ�����ͼ��Ķ���ΪM�����ı���AOCM�������
��3������������D��Eͬʱ�ӵ�O���������е�D��ÿ��![]() ����λ���ȵ��ٶ�������OAC��O��A��C��·���˶�����E��ÿ��4����λ���ȵ��ٶ�������OCA��O��C��A��·���˶�������D��E��������ʱ�����Ƕ�ֹͣ�˶�����D��Eͬʱ�ӵ�O����t��ʱ����ODE�����ΪS��
����λ���ȵ��ٶ�������OAC��O��A��C��·���˶�����E��ÿ��4����λ���ȵ��ٶ�������OCA��O��C��A��·���˶�������D��E��������ʱ�����Ƕ�ֹͣ�˶�����D��Eͬʱ�ӵ�O����t��ʱ����ODE�����ΪS��

������D��E�������˶������У��Ƿ����DE��OC�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
��ֱ��д��S����t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
���ڢ��У���t�Ƕ���ʱ��S�����ֵ�������������ֵ.
���𰸡���1��![]() ����2��10��3���ٲ�����DE��OC�ڵ�0��t��1ʱ��S��3t2����1��t��2ʱ��S��
����2��10��3���ٲ�����DE��OC�ڵ�0��t��1ʱ��S��3t2����1��t��2ʱ��S��![]() ����2��t��
����2��t��![]() ʱ��S����
ʱ��S����![]() ���۵�t��
���۵�t��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() .
.
�������������������1���ȸ���ֱ��AC�Ľ���ʽ���A��C��������꣬Ȼ�����A��B��C����������ô���ϵ����������������ߵĽ���ʽ��
��2�����������ߵĽ���ʽ�����M������꣬�����ı���OAMC���ǹ�����ı��Σ���˿ɹ�M��x��Ĵ��ߣ����ı���OAMC�ֳ�һ��ֱ�������κ�һ��ֱ����������⣮
��3�������DE��OC����ʱ��D��EӦ�ֱ����߶�OA��CA�ϣ�������������t��ȡֵ��Χ��Ȼ�����ƽ���߷��߶γɱ��������������ʱt��ֵ��Ȼ��t��ֵ�Ƿ���ϴ��������t��ȡֵ��Χ��������������t��ֵ���������ֵ����������ϣ���ô��˵��������������t��
�ڱ���Ҫ����������������ۣ�
��E��OC�ϣ�D��OA�ϣ�����0��t��1ʱ����ʱS=![]() OEOD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OEOD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
��E��AC�ϣ�D��OA�ϣ�����1��t��2ʱ����ʱS=![]() OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
��E��D����CA��ʱ������2��t��![]() ����ʱ�õ�ʱ�䣬��ʱS=S��AOE-S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ��
����ʱ�õ�ʱ�䣬��ʱS=S��AOE-S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ��
�����������ɵó���ͬ��t��ȡֵ��Χ�ڣ������IJ�ͬ����ʽ��
�۸��ݢڵĺ������ɵó�S�����ֵ��
�����������1������һ�κ���y����![]() x+4����x��0ʱ��y��4����y��0ʱ��x��3��
x+4����x��0ʱ��y��4����y��0ʱ��x��3��
��A��3��0����C��0��4����
����κ�����ϵʽΪy��ax2+bx+c��
��A��3��0����C��0��4����B����1��0������ã�
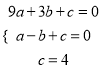 ����ã�
����ã� 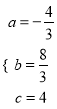 ��
��
����κ����Ĺ�ϵʽΪ![]() ��
��
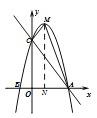
��2����![]() �ã�
�ã� ![]()
�������ߵĶ���M������Ϊ��1�� ![]() ����
����
����M��MN��x���ڵ�N����ON��1��MN��![]() ��
��
��A��3��0����C��0��4����
��OC��4��AN��3��1��2��
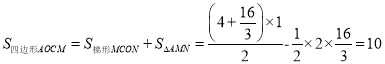
���ı���AOCN�����Ϊ10
��3���ٲ�����DE��OC��
����DE��OC����D��OA�ϣ�E��AC�ϣ���1��t��2��
��ʱ��OD��![]() ��AD��3��
��AD��3��![]() ��CE��4t��4��AE��9��4t��
��CE��4t��4��AE��9��4t��
��DE��OC���� ![]() ����
����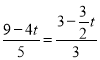 ��
��
��ã�t��![]()
��t��![]() ��2�������DE��OC��
��2�������DE��OC��
�ڵ�0��t��1ʱ��S��3t2��
��1��t��2ʱ��S��![]() ��
��
��2��t��![]() ʱ��S����
ʱ��S����![]() ��
��
����S��![]() ���ã�S��
���ã�S��![]() ��
��
��![]() ��0��
��0��
�൱t��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() .
.


