Question

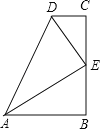
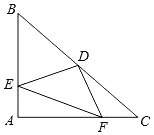
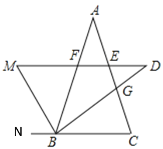
【题目】如图，△ABC中，AB＝AC，BD平分∠ABC交AC于G，DM∥BC交∠ABC的外角平分线于M，交AB、AC于F、E，下列结论：①MB⊥BD；②FD＝FB；③MD＝2CE．其中一定正确的是_____．（只填写序号）

Answer 1

【答案】①②③

【解析】

根据角平分线的定义即可证出∠MBD＝90°，从而证出①；根据角平分线、平行线和等腰三角形的关系即可证出②；同理可证MF＝BF，根据等边对等角即可证出：∠ABC＝∠ACB，然后根据平行线的性质可得：∠AFE＝∠ABC，∠AEF＝∠ACB，从而证出∠AFE＝∠AEF，再根据等角对等边即可证出AF＝AE，从而证出BF＝CE，即可证出③．

解：如图，∵BD、BM分别是∠ABC及其外角的平分线，

∴∠MBD＝∠MBA＋∠DBA=∠NBA＋∠CBA=（∠NBA＋∠CBA）=∠NBC=×180°＝90°，

故MB⊥BD，故①成立；

∵DF∥BC，

∴∠FDB＝∠DBC；

∵∠FBD＝∠DBC，

∴∠FBD＝∠FDB，

∴FD＝BF，故②成立；

同理可证MF＝BF，

∵AB＝AC，

∴∠ABC＝∠ACB，

∵DM∥BC，

∴∠AFE＝∠ABC，∠AEF＝∠ACB，

∴∠AFE＝∠AEF

∴AF＝AE，且AB＝AC，

∴BF＝CE，

∵DF＝BF，MF＝BF

∴MF＝DF

∵∠DBM＝90°，MF＝DF，

∴BF＝DM，而CE＝BF，

∴CE＝DM，③成立．

故答案为：①②③．