题目内容
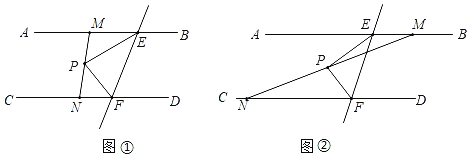
【题目】(问题)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.
【答案】(1)见解析;(2)见解析
【解析】
(1)由等腰直角三角形的性质可得∠CAB=∠CBA=45°,由平行线的性质可得∠CBA=∠DCB=45°,即可证DB=DP;(2)通过证明△CDP≌△GDB,可得DP=DB.
证明:(1)如图2
∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵CD∥AB
∴∠CBA=∠DCB=45°,且BD⊥CD
∴∠DCB=∠DBC=45°
∴DB=DC
即DP=DB;
(2)如图3
∵DG⊥CD,∠DCB=45°
∴∠DCG=∠DGC=45°
∴DC=DG,∠DCP=∠DGB=135°,
∵∠BDP=∠CDG=90°
∴∠CDP=∠BDG
在△CDP和△GDB中,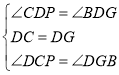
∴△CDP≌△GDB(ASA)
∴DP=DB.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目