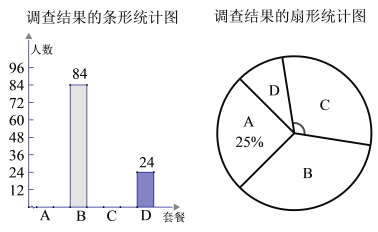
题目内容
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
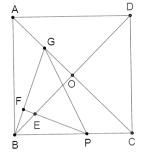
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,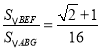 .
.
A.①②③B..①②④C.②③④D..①②③④
【答案】A
【解析】
①过G作GH⊥AB交于H点,得△BHG≌△BOG,HG=OG,解等腰直角三角形得![]() ;
;
②首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF=![]() BM,则可求得PE=2BF;
BM,则可求得PE=2BF;
③过P作PQ∥AC交BG于M,交BO于N,根据等腰直角三角形ABO的性质,可得![]() ,根据条件证得△PFG为等腰直角三角形,同理可证得
,根据条件证得△PFG为等腰直角三角形,同理可证得![]() ,由
,由![]() 即可证明;
即可证明;
④连接OP,则OP⊥BC,易知![]() ,根据①得
,根据①得![]() ,由△BEF∽△BGO,得
,由△BEF∽△BGO,得![]() ,进而得
,进而得![]() ,进而
,进而![]() ,整理即可求出结果.
,整理即可求出结果.
①过G作GH⊥AB交于H点,
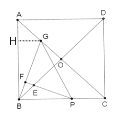
∵正方形ABCD,AC为对角线,
∴AG=![]() GH,
GH,
∵![]() ,
,![]() ,
,
∴△BHG≌△BOG,
∴HG=OG,
∴![]() ;
;
故①正确;
②如图2,过P作PM∥AC交BG于M,交BO于N,
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°∠BMN,∠NPE=90°∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中,
∠MBN=∠NPE,NB=NP,∠MNB=∠PNE=90°,
∴△BMN≌△PEN(ASA),
∴BM=PE,
∵∠BPE=
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中,∠BPF=∠MPF,PF=PF,∠PFB=∠PFM,
∴△BPF≌△MPF(ASA).
∴BF=MF,
即BF=![]() BM
BM
∴BF=![]() PE,即PE=2BE;
PE,即PE=2BE;
故②正确;
③过P作PQ∥AC交BG于M,交BO于N,
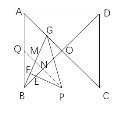
易知三角形ABO为等腰直角三角形,
设OG=x,则AG=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△GFP为等腰直角三角形,
同理,设MF=x,结合(1)的结论,
∴![]() ,
,
由(2)得,![]() ,
,
∴![]() ,
,
故③正确;
④连接OP,则OP⊥BC,
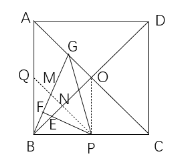
由(2)(3)可知,![]() 被均等分为四份,
被均等分为四份,
∴![]() ,
,
由(1)可知,![]() ,
,
∵![]() ,
,![]() ,
,
∴△BEF∽△BGO,
∴![]() ,
,
∵![]() ,
,
∴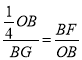
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴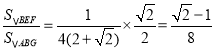 ,
,
故④错误;
故选:A.