题目内容
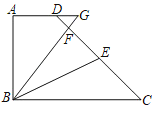
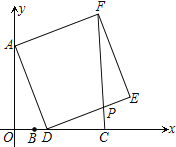
【题目】如图，在平面直角坐标系中，已知A（0，6），B（2，0），C（6，0），D为线段BC上的动点，以AD为边向右侧作正方形ADEF，连接CF交DE于点P，则CP的最大值_____．
【答案】
【解析】
过点F作FQ⊥y轴于Q，利用AAS证出△QFA≌△OAD，可得FQ=OA=6，从而得出FC⊥x轴，然后根据相似三角形的判定定理证出△OAD∽△CDP，列出比例式，然后设OD=x，由题意可知2≤x≤6，则CD=OC－OD=6－x，即可求出CP与x的二次函数关系，然后利用二次函数求最值即可．
解：过点F作FQ⊥y轴于Q
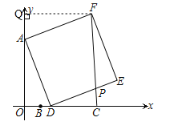
∴∠FQA=∠AOD=90°
∴∠OAD＋∠ODA=90°，
∵四边形ADEF为正方形
∴∠FAD=∠ADE=90°，FA=AD
∴∠OAD＋∠QAF=90°，∠ODA＋∠CDP=90°
∴∠QAF =∠ODA，∠OAD=∠CDP
∴△QFA≌△OAD
∴FQ=OA=6
∴点F的横坐标为6
∵C（6，0），
∴FC⊥x轴
∴∠AOD=∠DCP=90°
∵∠OAD=∠CDP
∴△OAD∽△CDP
∴
设OD=x，由题意可知2≤x≤6，则CD=OC－OD=6－x
∴
解得：CP=
∴当x=3时，CP最大，最大值为
故答案为：．
练习册系列答案
小题狂做系列答案
相关题目
