Question

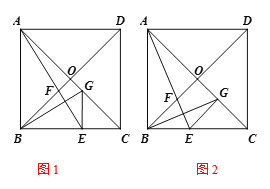
【题目】如图1，在正方形ABCD中，点O是对角线AC，BD的交点，点E在BC边上(点E不和BC的端点重合)，且BE＝BC，连接AE交OB于点F，过点B作AE的垂线BG交OC于点G，连接GE．

（1）求证：OF＝OG；

（2）用含的代数式表示tan∠OBG的值；

（3）如图2，当∠GEC＝90°时，求的值．

Answer 1

【答案】（1） 证明见解析；（2）；（3）．

【解析】

（1）由正方形的性质可得AO＝BO，AC⊥BD，由余角的性质可得∠FAO＝∠FBG，由“ASA”可证△AOF≌△BOG，可得OF＝OG；

（2）根据第一问条件推导出FG∥BC∥AD，从而由平行线分线段成比例得到，通过已知条件可推断AG＝GC，设GC＝，并表示其他线段即可解决问题；

（3）根据第二问结论，使OG用OC来表示，进而使GC用BC来表示，另根据BE＝BC可得EC＝BC，从而用BC表示CG，列出方程即可解决问题.

解：（1）证明：∵四边形ABCD是正方形，

∴OA＝OB，AO⊥BO，

由∵AE⊥BG，∴∠OAF＝∠OBG，

∴Rt△AOF≌Rt△BOG，

∴OF＝OG；

（2）

连接FG，

∵OF＝OG，AC⊥BD，

∴∠OGF＝45°＝∠OCB，∴FG∥BC∥AD，

∴，

∵BE＝BC＝AD，

∴AG＝GC，

设GC＝，则AG＝，AC＝，

∴OB＝OC＝AC＝，

OG＝OC－GC＝，

∴tan∠OBG＝＝；

（3）解：如图，

当∠GEC＝90°时，∵∠GCE＝45°，

∴△GEC是等腰直角三角形，

∴GC＝EC，

∵tan∠OBG＝＝，

∴OG＝OB＝OC，

∴GC＝OC－OG＝OC

＝BC，

又∵BE＝BC，

∴EC＝BC－BE＝BC，

∴BC＝BC，

即：，

解得：或(舍去)，

故．