题目内容
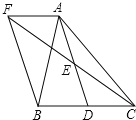
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC,AO=DO,直线y=mx+1与y轴交于点D.
(1)求抛物线和直线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

【答案】(1)y=﹣![]() x+1,y=x2﹣2x﹣3(2)证明见解析(3)P(1,﹣1)或P(1,
x+1,y=x2﹣2x﹣3(2)证明见解析(3)P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() )
)
【解析】分析:(1)抛物线![]() ,求出
,求出![]() 即可求得点
即可求得点![]() 的坐标,根据
的坐标,根据![]() ,求得点
,求得点![]() 的坐标,代入一次函数
的坐标,代入一次函数![]() 即可确定一次函数解析式,进而求得点
即可确定一次函数解析式,进而求得点![]() 的坐标,根据
的坐标,根据![]() 求得点
求得点![]() 的坐标,根据待定系数法即可确定二次函数解析式.
的坐标,根据待定系数法即可确定二次函数解析式.
(2)先把抛物线解析式配成顶点式得到E(1,-4),再利用一次函数解析式确定D(0,1),则利用两点间的距离公式可计算出![]()
![]()
![]() 而得到
而得到![]() 然后根据相似三角形的判定方法可判断
然后根据相似三角形的判定方法可判断![]()
(3)设设P(1,m),则利用两点间的距离公式可得![]()
![]()
![]() 然后分类讨论即可.
然后分类讨论即可.
详解:(1)∵抛物线![]() ,
,![]()
∴![]()
∵![]()
![]()
把![]() 代入
代入![]() 得
得![]()
∴直线解析式为![]() ,
,
∵直线![]() 与y轴交于点D,
与y轴交于点D,![]()
∵![]()
![]()
∵该抛物线与x轴交于A、B两点,
![]() 解得:
解得:![]()
∴抛物线解析式为![]()
(2)证明:∵
![]()
∴E(1,4),
当x=0时, ![]() ,则D(0,1),
,则D(0,1),
∵B(3,0),A(1,0),C(0,3),
∴![]()
![]()
∵![]()
∴![]()
∴△BCE∽△BDO;
(3)存在,
理由:抛物线的对称轴为直线x=1,设P(1,m),则![]()
当PB=PC时,△PBC是等腰三角形,则m2+4=(m+3)2+1,解得m=1,此时P(1,1),
当PB=BC时,△PBC是等腰三角形,则m2+4=18,解得![]() 此时
此时![]() 或
或![]()
当PC=BC时,△PBC是等腰三角形,则(m+3)2+1=18,解得![]() 此时
此时![]() 或
或![]()
综上所述,当符P点坐标为(1,1)或![]() 或
或![]() 或
或![]() 或
或![]() 时,△PBC是等腰三角形。
时,△PBC是等腰三角形。

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案